Geometria
Blue: zad.6 Napisz równania prostych przechodzących przez punkt P=(3,2) i odcinających na osiach
układu współrzędnych odcinki OA i OB takie, że pole trójkąta AOB jest równe 12.
| | −2 | |
Wyszło mi tylko y= |
| x+4, a w odpowiedziach mam więcej prostych. |
| | 3 | |
zad.12 Wyznacz równania prostych zawierających dwusieczne kątów utworzonych przez proste
2x−y+1=0 i x−2y+2=0.
Mi wyszło y= −x+1 i y=x+1.
Co niestety jest źle.
Proszę o pomoc

7 gru 11:13
7 gru 11:32
Kacper:
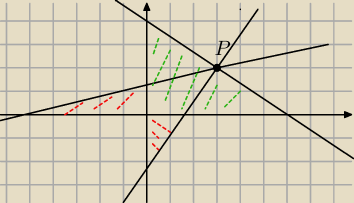
Ty masz zielony trójkąt, a są jeszcze 2 czerwone

7 gru 11:36
Blue: Tylko Kacper ja do zadania 12 mam jakąś dziwną odp: x2=(y−1)2 lub |x|=|y−1|
7 gru 11:55
===:
... zadanie 6 to bardzo fajne zadanko −

"interdyscyplinarne" jak zadanka na nową
maturę rozszerzoną. Ale chyba i na rozszerzenie to dość trudne −

7 gru 12:02
Kacper:
|y−1|=|x| ⇔ y−1=x lub y−1=−x ⇔ y=x+1 lub y=−x+1
Przecież masz taką samą odpowiedź

7 gru 12:09
Blue: hahah xd nie mogę xD Czyli Mam to dobrze

Kacper, ale ja to inaczej liczyłam

7 gru 12:16
Blue: Wyznaczyłam sobie 3 punkty i potem środki odcinków między tymi punktami i .... chyba musiałabym
Ci to zeskanować, ale w sumie sposób nie jest ważny, ważne, że dobrze wyszło

7 gru 12:17
Kacper:
Sposób jest ważny, bo mogą być jakieś błędy merytoryczne, a czasem odpowiedź się zgadza

7 gru 12:21
===:
Przemycę do niego odcinkowe równanie prostej (troszkę zapomniane)
Piszemy równanie pęku prostych przez punkt P
y−2=a(x−3) ⇒ y=ax−3a+2
i przekształcamy do postaci odcinkowej
i teraz "modułki" −

| | (3a−2)2 | |
| |
| |=12 ....dalej już dla Ciebie −  |
| | a | |
7 gru 12:23
Blue: To Ci potem skseruję to

7 gru 12:24
===:
... nasz może odpowiedzi do tego zadanka ? (nr 6)
7 gru 12:25
===:
... no tak ...spaprałem −:(
=24 ....a nie 12
7 gru 12:28
Kacper:
Ja znam odpowiedzi

(pierwiastki dostajemy w pozostałych przypadkach

)
7 gru 12:28
Blue: | | 4 | |
Już piszę odpowiedzi: y= (2− |
| √2)x−(4−4√2) |
| | 3 | |
7 gru 12:50
===:
... na właśnie
Kacper ... Twoje rysunki nie oddają tych prostych −

7 gru 13:01
===:
... z mego równania wychodzi
czyli dokładnie jak w odpowiedziach −

7 gru 13:05
Kacper:
No mój rysunek jest tylko szkicowy

Nie zmieszczą się te proste

7 gru 13:05
===:
zmieszczą ...zmieszczą −

7 gru 13:09
===:
... to ciekawe zadanie ... chyba warto więc je dokończyć
od momentu
(3a−2)
2=24a lub (3a−2)
2=−24a
9a
2−36a+4=0 9a
2+12a+4=0
| | 2 | |
Δ=1152 √Δ=24√2 (3a+2)2=0 ⇒ a3=− |
| ]] |
| | 3 | |
7 gru 13:25
===:
oj... i wysłało się −:(
7 gru 13:26
===:
...
Blue dokończy −

7 gru 13:26
Mila:
Odpowiedzi do 12?
7 gru 18:45
Mila:
?
7 gru 23:22
Blue: Podałam już wyżej, zaraz wrzucę skan swojego rozwiązania
7 gru 23:25
7 gru 23:28
Mila:
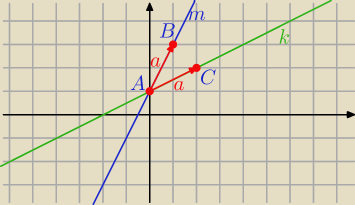
12 Dobrze zrobiłaś. Można też wektorowo.
2x−y+1=0 i x−2y+2=0.⇔
m: y=2x+1
k: y=Y{1}{2}x+1
A(0,1) punkt przecięcia prostych.
B=(1,3) ∊m
C=(2, 2)∊k
AB
→=[1,2]
AC
→=[2,1]
|AB|=
√1+4=
√5
|AC|=
√5
wektory o równej długości⇔można zbudować romb ACDB i przekątna rombu jest dwusieczną kąta BAC.
AD
→=AB
→+AC
→=[1,2]+[2,1]= [3,3] wektor równoległy do dwusiecznej ∡BAC
n→=[3,−3] wektor prostopadły do dwusiecznej
3x−3y+C=0 i (0,1)∊dwusiecznej
−3+C=0, C=3
3x−3y+3=0⇔x−y+1=0
d
1: y=x+1
d
2: y=−x+1
7 gru 23:34
7 gru 23:42
Blue: To rozwiązanie, które podał ===(Tadeusz) jest jedyne czy można to inaczej liczyć

Jeśli tak,
to proszę o pokazanie rozwiązania do zad 6

9 gru 21:57
Kacper:
Oczywiście jest dobrze. Ja bym napisał tak:
∡MBA+∡NBA=∡NBM
|∡MBA|=90o
|∡NBA|=90o
Zatem |∡NBM|=180o ⇒ Punkty N, B, M są współliniowe. c.n.u.
9 gru 22:03
Blue: Kacper o czym Ty mówisz?
9 gru 22:10
Kacper:
A o co ty pytasz? Sama robisz takie zamieszanie, a potem nie wiesz co jest co. Pytasz w 5
tematach o inne zadania

9 gru 22:13
Blue: o zadanie numer 6

Kacper nie denerwuj się

9 gru 22:15
Blue: Pytam o to zadanie, do którego zrobiłeś rysunek

9 gru 22:17
Kacper:
To dostałaś moją odpowiedź na temat zadania 6

9 gru 22:18
Blue: no ale rysunek mi mało mówi.... mi wyszła tylko jedna prosta dobrze
9 gru 22:31
Mila:
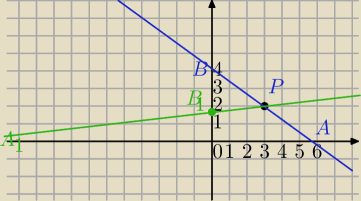
Zadanie 6.
B=(0,b)
A=(x
x,0)
Prosta AB: y=ax+b
2=3a+b
b=2−3a
y=ax+2−3a
Miejsce zerowe:
ax+2−3a=0
ax=3a−2
| | 1 | | 3a−2 | | |3a−2|2 | |
P= |
| *| |
| |*|2−3a|= |
| ⇔ |
| | 2 | | a | | 2a | |
|3a−2|
2=24|a|
9a
2−12a+4=24a lub 9a
2−12a+4=−24a
Dokończ
10 gru 00:24
Kacper:
Blue weź się ogarnij, bo przestane ci pomagać

10 gru 08:55
Mila:
Kacper, spokojnie nie denerwuj się. Trochę ją przetrzymujemy z podpowiedziami i
rozwiązaniami, to też musi dokończyc sama.
Jak Ci leci w szkole?.Będą u Ciebie pisać maturę próbną CKE?
10 gru 14:54
Blue: Kacper, ostatnio mam już wszystkiego dość, więc wybacz, przez święta spróbuję się ogarnąć...
Mila, tak, w przyszłym tygodniu w czwartek piszę rozszerzenie

10 gru 17:21
Blue: A więc tak to trzeba rozwiązać

Dzięki

Mila, tam przy a w mianowniku zapomniałaś dać
wartości bez., ale to szczególik i na początku napisałaś x
x zamiast x
0
10 gru 17:26
Mila:
No, tak − literówki, co innego się myśli , co innego naciska. Dobrze skorygowałaś.
Napiszesz dobrze. Nie martw się. Robisz duże postępy.
10 gru 17:38
Blue: Wyszło mi tak jak w odpowiedziach

10 gru 17:41
Blue: Dzięki za wsparcie Mila

10 gru 17:42

 Ty masz zielony trójkąt, a są jeszcze 2 czerwone
Ty masz zielony trójkąt, a są jeszcze 2 czerwone 
 "interdyscyplinarne" jak zadanka na nową
maturę rozszerzoną. Ale chyba i na rozszerzenie to dość trudne −
"interdyscyplinarne" jak zadanka na nową
maturę rozszerzoną. Ale chyba i na rozszerzenie to dość trudne −

 Kacper, ale ja to inaczej liczyłam
Kacper, ale ja to inaczej liczyłam 





 (pierwiastki dostajemy w pozostałych przypadkach
(pierwiastki dostajemy w pozostałych przypadkach  )
)


 Nie zmieszczą się te proste
Nie zmieszczą się te proste 



 12 Dobrze zrobiłaś. Można też wektorowo.
2x−y+1=0 i x−2y+2=0.⇔
m: y=2x+1
k: y=Y{1}{2}x+1
A(0,1) punkt przecięcia prostych.
B=(1,3) ∊m
C=(2, 2)∊k
AB→=[1,2]
AC→=[2,1]
|AB|=√1+4=√5
|AC|=√5
wektory o równej długości⇔można zbudować romb ACDB i przekątna rombu jest dwusieczną kąta BAC.
AD→=AB→+AC→=[1,2]+[2,1]= [3,3] wektor równoległy do dwusiecznej ∡BAC
n→=[3,−3] wektor prostopadły do dwusiecznej
3x−3y+C=0 i (0,1)∊dwusiecznej
−3+C=0, C=3
3x−3y+3=0⇔x−y+1=0
d1: y=x+1
d2: y=−x+1
12 Dobrze zrobiłaś. Można też wektorowo.
2x−y+1=0 i x−2y+2=0.⇔
m: y=2x+1
k: y=Y{1}{2}x+1
A(0,1) punkt przecięcia prostych.
B=(1,3) ∊m
C=(2, 2)∊k
AB→=[1,2]
AC→=[2,1]
|AB|=√1+4=√5
|AC|=√5
wektory o równej długości⇔można zbudować romb ACDB i przekątna rombu jest dwusieczną kąta BAC.
AD→=AB→+AC→=[1,2]+[2,1]= [3,3] wektor równoległy do dwusiecznej ∡BAC
n→=[3,−3] wektor prostopadły do dwusiecznej
3x−3y+C=0 i (0,1)∊dwusiecznej
−3+C=0, C=3
3x−3y+3=0⇔x−y+1=0
d1: y=x+1
d2: y=−x+1

 Jeśli tak,
to proszę o pokazanie rozwiązania do zad 6
Jeśli tak,
to proszę o pokazanie rozwiązania do zad 6 

 Kacper nie denerwuj się
Kacper nie denerwuj się 


 Zadanie 6.
B=(0,b)
A=(xx,0)
Zadanie 6.
B=(0,b)
A=(xx,0)


 Dzięki
Dzięki  Mila, tam przy a w mianowniku zapomniałaś dać
wartości bez., ale to szczególik i na początku napisałaś xx zamiast x0
Mila, tam przy a w mianowniku zapomniałaś dać
wartości bez., ale to szczególik i na początku napisałaś xx zamiast x0

