Planimetria
Blue: Zadanka z planimetrii:
zad.1 W czworokącie ABCD kąt ADC ma miarę 30
0 oraz |AB|=3, |BC|=4, |AC|=6. Uzasadnij, że na
tym czworokącie nie można opisać okręgu.
zad.2 Udowodnij, że suma odległości dowolnego punktu leżącego na podstawie trójkąta
równoramiennego do jego ramion nie zależy od wyboru tego punktu. − zdanie trochę niepoprawne
gramatycznie, ale tak jest w książce.
zad.3 W trójkącie o bokach długości a, b, c środkowe poprowadzone do boków a i b są do siebie
prostopadłe. Udowodnij, że a
2+b
2=5c
2
zad.4 Na zewnątrz kwadratu na jednym z jego boków skonstruowano trójkąt prostokątny.
Przeciwprostokątna tego trójkąta pokrywa się z bokiem kwadratu. Udowodnij, że dwusieczna kąta
prostego tego trójkąta dzieli pole kwadratu na połowy.
zad.5 W trójkąt prostokątny wpisano prostokąt (patrz rysunek). Uzasadnij, że pole prostokąta
| | 1 | |
nie może być większe od |
| S. |
| | 2 | |
zad.6 Dwa okręgi przecinają się w punktach A i B. Uzasadnij, że jeśli AM i AN są średnicami
tych okręgów, to punkty M,B,N leżą na jednej prostej.
Rozwiązałam zadanie 1, 3,4,5

− ale zadanie 5 na pewno jest źle

Oto skany:
http://i57.tinypic.com/9hhqbc.jpg
http://i58.tinypic.com/vy5tu8.jpg
http://i58.tinypic.com/n3kl7s.jpg
http://i57.tinypic.com/rwjj48.jpg
Rysunek do zad.6 i 5 :
http://i59.tinypic.com/2j2wc1v.jpg
Bardzo proszę o ocenę, czy takie dowody mogą być i o wyjaśnienie zadań, których nie umiałam
zrobić

5 gru 16:42
Mila:
1) Warunkiem koniecznym, aby na tym czworokącie można było opisać okrąg jest,
aby ∡ABC=180
o−30
o=150
0
| | √3 | |
cos(150o)=cos(180o−300)=−cos 30o=− |
| |
| | 2 | |
Z tw. cosinusów w ΔABC:
| | √3 | |
cos∡ABC= ...≠− |
| ⇔Na czworokącie ABCD nie można opisać okręgu. |
| | 2 | |
5 gru 19:25
Mila:

2) Podpowiedź będzie .
dokończ
5 gru 20:02
Blue: czyli a*h=x+y.... i z tego wynika, że nie zależy to od tego punktu, bo zawsze suma wynosi a*h

5 gru 20:32
Blue: a 3 i 4 jest udowodnione?
5 gru 20:33
5 gru 20:37
Mila:
3) Może być, ale pisz założenie , teza, w jakim Δ stosujesz tw. Pit.
5 gru 20:45
Mila:
4) coś tam trzeba dodać.
6) Masz tam dwa kąty wpisane oparte na średnicy.
5 gru 21:04
Blue: | | a*h | |
sorki, oczywiście, że x+y = |
| , ale takie coś wystarczy? |
| | b | |
5 gru 21:45
Mila:
Tak.
5 gru 21:49
Blue: Dziękuję Milu

A co z zadaniami 4,5,6? Co byś tam jeszcze dopisała w tym 4? Ale w tym 6
przecież ten trójkąt nie jest równoramienny, prawda?
6 gru 10:35
Tadeusz:
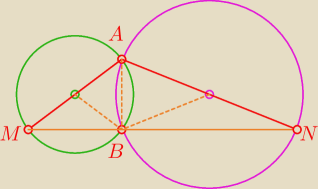
oba kąty czyli ∡ABM jak i ∡ABN są proste jako oparte na średnicy okręgu
... a skoro mają wspólne ramię AB ...
6 gru 10:48
Blue: Nie wiem, jak to wykazać, niby to jest oczywiste, że leżą na wspólnej prostej, ale co ja mam
tutaj napisać

90
0+90
0=180
0 czyli punkty leżą na jednej prostej?
6 gru 11:49
Kacper: 
6 gru 11:50
Tadeusz:
... tak proste, że aż trudne

?

6 gru 12:04
Kacper:
Zazwyczaj

6 gru 12:16
Blue: Czyli w końcu jak ma wyglądać ten dowód

6 gru 12:19
Tadeusz:
jeśli dwa kąty proste mają wspólne ramię ...
6 gru 12:24
Blue: to tworzą prostą?

6 gru 12:29
J:
..popatrz na to tak, jesli np. dwa kąty po 30o mają wspólne ramię,
to pozostałe ramiona tworzą kąt 60o
..jeśli mają zatem mają po 90o , to pozostałe tworzą kąt 180o ( leżą w jwdnej prostej)
6 gru 12:30
Blue: dzięki J

6 gru 16:10
Mila:
Blue, kąty przyległe, kąty wierzchołkowe, środkowe, wpisane w okrąg. ⇔powtórka z SP i GM.
6 gru 18:22
Blue: No to pozostało nam tylko 5 zadanko

6 gru 21:20
Blue: No i co mam dopisać jeszcze w tym 4?

6 gru 21:32
Kacper:
Zadanie 5 zrobiłaś "na oko"

Trzeba to uzasadnić przy użyciu narzędzi matematycznych

6 gru 21:49
Kacper:
W zadaniu 4 uzasadnić należy twoje stwierdzenie "suma krótszej podstawy jednego trapezu z
dłuższą podstawą
musi być taka sama..."
Nic
blue nie musi

Tak jest, ale dlaczego?
6 gru 21:53
Blue: no właśnie wiem, ale wolałam coś napisać, niż nic ...czyli jak zrobić to 5

w 4 musi bo to jest bok kwadratu
6 gru 21:57
Kacper:
Dzieli na pół?

6 gru 22:00
Kacper:
Zadanie 5 skojarz z zadaniami optymalizacyjnymi i pokaż, że maksymalne pole prostokąta wynosi
połowę pola trójkąta

6 gru 22:01
Blue: no nie dzieli .. czyli o coś innego chodzi..
6 gru 22:12
Blue: eh.... chyba nic tutaj nie wymyślę. Czekam na rozwiązanie.
6 gru 22:35
Kacper:
Daj sobie dzisiaj spokój i wrócisz jutro

6 gru 22:37
Mila:
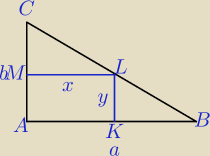
P
AKLM=x*y
ΔCML∼ΔCAB⇔
| | b | | b | |
PAKLM(x)=x* |
| *(a−x)= |
| *(ax−x2) |
| | a | | a | |
| | a | | a | |
xw= |
| dla x= |
| pole prostokąta jest największe |
| | 2 | | 2 | |
| | a | | b | | a2 | | a2 | | ab | | 1 | |
P( |
| )= |
| *( |
| − |
| )= |
| = |
| S⇔ |
| | 2 | | a | | 2 | | 4 | | 4 | | 2 | |
6 gru 23:11
Blue: Dziękuję Mila

7 gru 12:29
Blue: Liczę jeszcze na pełne wyjaśnienie 4

7 gru 12:29
Blue: Mógłby ktoś rozwiązać to 4 ?

Proszę

7 gru 23:06
Mila:
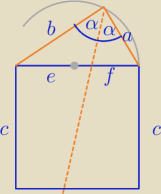
Skorzystaj z własności dwusiecznej.
α=45
o
8 gru 00:01
8 gru 00:28
Blue: Mila, co ja mam tutaj zrobić?
8 gru 18:47
Blue: :(
8 gru 20:19
Blue: Pokaże ktoś pełny dowód tego 4 ?
8 gru 20:26
Kacper:
2 dni i nie wymyśliłaś ?

8 gru 20:27
===:
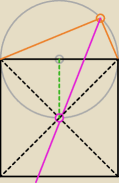
... a teraz widzisz? −

8 gru 20:29
===:
... nie ładnie. "Popłaczesz" ... "popłaczesz" i pójdziesz. Zawsze chcesz trzymać trzy sroki

?
−

8 gru 20:58
===:
... to jeszcze przedłuż tą zieloną przerywaną i wszystko będzie jasne −

8 gru 21:06
Blue: ja nie płaczę

8 gru 21:14
Blue: Tam powstaną dwa trójkąty przystające... i co z tego?
8 gru 21:18
===:
... sedno programu polega na tym, że masz zauważyć ... udowodnić i wykorzystać fakt, że
ta dwusieczna przechodzi przez środek kwadratu.
8 gru 21:30
Blue: aaaa
8 gru 21:30
Blue: ale w sumie, to jak ja mam udowodnić, że ona przechodzi przez ten środek...
8 gru 21:32
===:
... twierdzenie o kącie środkowym i wpisanym −

8 gru 21:35
===:
... troszkę "wpuściła" Cię
Mila z tym wykorzystaniem dwusiecznej −

8 gru 21:40
Blue: Czy masz na myśli to, że ten kąt trójkąta wewnątrz kwadratu jest podzielony na dwa kąty równe
kątom ostrym trójkąta umieszczonego na boku, bo są oparte na tym samym łuku?
8 gru 21:43
===:
nie
Masz wykazać, że dwusieczna przechodzi przez środek kwadratu
8 gru 21:47
Blue: ale problem polega na tym, że nie wiem, jak to zrobić....
8 gru 21:50
Blue: === zlitowałbyś się i napisał rozwiązanie

8 gru 21:52
===:

8 gru 21:56
===:
... to tak proste, że aż trudne
∡AD0 jest kątem prostym (środkowy oparty na łuku A0)
Jeśli ∡ACH ma 45o i jest kątem wpisanym opartym jednym ramieniem w punkcie A
to musi być oparty na łuku A0
8 gru 22:02
===:
na przedłużeniu zielonej zaznacz punkt E (który "zjadłem")
ΔDG0 i ΔEH0 są przystające ... jasne więc, że dwusieczna dzieli kwadrat na połowy
8 gru 22:05
Tadeusz:
... to TY nie wiesz jak mam na imię tylko przezywasz mnie od === −

8 gru 22:07
Blue: hm....
8 gru 22:10
Kacper:
Nie bardzo rozumiem
Tadeusz?

8 gru 22:13
Blue: sorki nie załadowały mi się jeszcze komentarze, jak pisałam ostatni komentarz

Czyli wystarczy, że zrobię ten rysunek i napiszę Twój komentarz i to będzie już dowód


8 gru 22:14
Blue: Skąd miałam wiedzieć, że to Ty, Tadeuszu?

Nie jestem jasnowidzem

8 gru 22:14
Tadeusz:
... skoro pytasz czy wystarczy ... to chyba nie do końca rozumiesz
Powiedz czego nie rozumiesz?
8 gru 22:16
Blue: niby rozumiem, jakoś nie jestem pewna czy to wykazaliśmy
8 gru 22:19
Tadeusz:
czy DE dzieli kwadrat na połowy ?
8 gru 22:22
Blue: tak
8 gru 22:23
Tadeusz:
czy CH może przeciąć DE w innym punkcie niżeli 0?
8 gru 22:23
Blue: no nie bo kąt przy wierzchołku C wynosi 90 stopni

8 gru 22:26
Blue: sorry 45 stopni chciałam napisać, tzn kąt ACH

8 gru 22:26
Tadeusz:
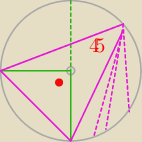
8 gru 22:30
Blue: no czyli wszystko już jasne?

8 gru 22:38
Tadeusz:
... mnie pytasz

?
Skoro CH przecina DE w punkcie 0 ....czyli w połowie to ΔDGO i ΔEHO są przystające
(w innym przypadku byłyby tylko podobne) ...a skoro przystające to wszystko jasne
(powstałe trapezy są przystające)
8 gru 22:45
Blue: ok, dziękuję

8 gru 22:52
Tadeusz:
..."zaskoczyłam"

? −

8 gru 23:02
Kinga: Hej Blue. Chciałam cię tylko zapytać z jakiej książki są te zadania?Fajnie, jeśli mogłabyś mi
napisać jej tytuł i autora. Będę wdzięczna

.
30 gru 16:38
Alle18: Testy maturalne wydawnictwo Aksjomat
Autorzy: Dorota Maslowska, Tomasz Maslowski, Piotr Nodzynski, Elzbieta Slominska, Alicja
Strzelczyk.
13 kwi 01:05
 − ale zadanie 5 na pewno jest źle
− ale zadanie 5 na pewno jest źle  Oto skany:
http://i57.tinypic.com/9hhqbc.jpg
http://i58.tinypic.com/vy5tu8.jpg
http://i58.tinypic.com/n3kl7s.jpg
http://i57.tinypic.com/rwjj48.jpg
Rysunek do zad.6 i 5 :
http://i59.tinypic.com/2j2wc1v.jpg
Bardzo proszę o ocenę, czy takie dowody mogą być i o wyjaśnienie zadań, których nie umiałam
zrobić
Oto skany:
http://i57.tinypic.com/9hhqbc.jpg
http://i58.tinypic.com/vy5tu8.jpg
http://i58.tinypic.com/n3kl7s.jpg
http://i57.tinypic.com/rwjj48.jpg
Rysunek do zad.6 i 5 :
http://i59.tinypic.com/2j2wc1v.jpg
Bardzo proszę o ocenę, czy takie dowody mogą być i o wyjaśnienie zadań, których nie umiałam
zrobić 
 2) Podpowiedź będzie .
2) Podpowiedź będzie .

 A co z zadaniami 4,5,6? Co byś tam jeszcze dopisała w tym 4? Ale w tym 6
przecież ten trójkąt nie jest równoramienny, prawda?
A co z zadaniami 4,5,6? Co byś tam jeszcze dopisała w tym 4? Ale w tym 6
przecież ten trójkąt nie jest równoramienny, prawda?
 oba kąty czyli ∡ABM jak i ∡ABN są proste jako oparte na średnicy okręgu
... a skoro mają wspólne ramię AB ...
oba kąty czyli ∡ABM jak i ∡ABN są proste jako oparte na średnicy okręgu
... a skoro mają wspólne ramię AB ...
 900+900=1800 czyli punkty leżą na jednej prostej?
900+900=1800 czyli punkty leżą na jednej prostej?

 ?
? 






 Trzeba to uzasadnić przy użyciu narzędzi matematycznych
Trzeba to uzasadnić przy użyciu narzędzi matematycznych 
 Tak jest, ale dlaczego?
Tak jest, ale dlaczego?
 w 4 musi bo to jest bok kwadratu
w 4 musi bo to jest bok kwadratu
 Dzieli na pół?
Dzieli na pół? 





 Proszę
Proszę
 Skorzystaj z własności dwusiecznej.
α=45o
Skorzystaj z własności dwusiecznej.
α=45o

 ... a teraz widzisz? −
... a teraz widzisz? −
 ?
−
?
−








 Czyli wystarczy, że zrobię ten rysunek i napiszę Twój komentarz i to będzie już dowód
Czyli wystarczy, że zrobię ten rysunek i napiszę Twój komentarz i to będzie już dowód

 Nie jestem jasnowidzem
Nie jestem jasnowidzem 




 ?
Skoro CH przecina DE w punkcie 0 ....czyli w połowie to ΔDGO i ΔEHO są przystające
(w innym przypadku byłyby tylko podobne) ...a skoro przystające to wszystko jasne
(powstałe trapezy są przystające)
?
Skoro CH przecina DE w punkcie 0 ....czyli w połowie to ΔDGO i ΔEHO są przystające
(w innym przypadku byłyby tylko podobne) ...a skoro przystające to wszystko jasne
(powstałe trapezy są przystające)

 ? −
? −
 .
.