pochodne kyrtap: Mila wiesz gdzie są dość jasno wytłumaczone tego typu przykłady https://matematykaszkolna.pl/forum/267753.html

Mila: Nie przypominam sobie. Nie masz w książce przykładów? Jedyne tłumaczenie, to takie jak podał PW, liczymy granicę ilorazu różnicowego, ale ja liczę granicę takiego ilorazu:

	f(x0+h)−f(x0)
limh→0
	h

Zbadaj czy istnieje pochodna : a) f(x)=|x| w punkcie x₀=0 b) f(x)=3x²+4x dla x≤−2 −8x−12 dla x>−2 w punkcie x₀=−2

kyrtap: tylko czasami nie wiem czy potem ten lim liczyć w punkcie z prawej od punktu czy z lewej jak jest wartość bezwzględna to wiadomo

Mila: Jeśli funkcja sklejana to dwie granice, jeśli są "szpice" to na ogół dwie granice − prawostronną i lewostronną, jeśli masz przykład f(x)=x³ i x₀=2, to od razu widać, że liczysz jedną granicę ilorazu różnicowego. Argument x=2 nie jest "podejrzany".

Gray: Reguła jest prosta: jeżeli masz funkcję zdefiniowaną przez tzw. klamerkę (rozbitą na przypadki), to w punkcie (lub w punktach) w którym następuje rozbicie (czyli zmiana wzoru) pochodną zawsze możesz liczyć z definicji (tak będzie najbezpieczniej). I zawsze możesz liczyć te pochodne jako pochodne jednostronne. Jeżeli będą one równe − funkcja będzie różniczkowalna w punkcie, jak nie to nie. Jak nabierzesz wprawy, będziesz wiedział, które przypadki musisz koniecznie liczyć z definicji, a które możesz z definicji, a możesz i normalnie. Funkcja |x| nie jest w tym przypadku żadnym wyjątkiem. W x₀=0 możesz liczyć pochodne jednostronne z definicji. I będzie OK. O ile, rzecz jasna, się nie pomylisz.

kyrtap: rozwiąże ten b) i spr czy dobrze pojmuje

	⎧	3x2 + 4x dla x≤−2
f(x) =	⎨		x0 = −2
	⎩	−8x−12 dla x>−2

	f(x) − f(−2)		−8x−12 − 4
liczę pochodną f'+(−2) = limx→−2+		= limx→−2+		=
	x+2		x+2

	−8(x+2)
limx→−2+		= −8
	x+2

	3x2 + 4x − (3(−2)2 + 4(−2))
f'(−2) = limx→−2		=
	x+2

	3x2 + 4x − 12 +8		3x2 +4x −4
limx→−2		= limx→−2		i co teraz bo nie wiem
	x+2		x+2

co dalej zrobić

Gray: Mila Cię poprowadzi, nie będę się wtrącał, ale jedno pytanie tylko: to f(−2), które masz w liczniku przy pochodnej f'₊(−2) to z którego wzoru liczyłeś? Z dolnego, czy górnego? No i przy drugiej pochodnej powinno być f'₋(−2) = ...

kyrtap: z dolnego liczyłem

Gray: Tak sądziłem. Nie możesz z dolnego, bo dolny działa jedynie dla x>−2. Górny jest dla x≤−2.

Mila: Δ i rozkład na iloczyn.

kyrtap: czyli co muszę obliczyć granicę lewostronną i prawostronną dla 3x² + 4x

Gray: Nie. Liczysz pochodną funkcji f, a nie 3x³+4x. Tę funkcję wykorzystujesz jedynie przy pochodnej lewostronnej funkcji (bo ona tylko dla x≤−2). No i ona dostarcza informacji o wartości f(x) w punkcie x=−2. Dobrze liczyłeś to co napisałeś. Jedynie f(−2)=3(−2)²+4(−2) = 4. U Ciebie wychodzi to samo, ale nie zawsze tak musi być.

kyrtap: wyszło f'(−2) = −8 ok załóżmy że tylko to liczyłem i nic więcej wyszło mi −8 i co stwierdzam z tego faktu

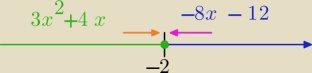
Mila: Po narysowaniu osi i zaznaczeniu dziedziny obu funkcji widzisz jakie granice trzeba liczyc.

kyrtap: no ok wyszło f'(−2) = −8 i co w związku z tym

Gray: Skoro f'₋(−2) = f'₊(−2)=−8 to f'(−2) = −8. Czyli funkcja f jest wszędzie różniczkowalna.

kyrtap: Gray nie kumam, pytałem czy liczyć granice jednostronne to napisałeś że nie to czemu tutaj napisałeś że f'₋ (−2) = f'₊(−2)

kyrtap: dobra już chyba wiem o co Tobie chodzi dzięki wam

Mila: Liczysz granicę lewostronną w x₀=−2 ilorazu różnicowego dla funkcji y=3x²+4x ( z prawej strony (−2) ta funkcja nie jest określona) i Liczysz granicę prawowostronną ilorazu różnicowego dla funkcji y=−8x−12 w x₀=−2 Jeżeli istnieją granice i są równe, to f(x) jest różniczkowalna w x=−2.