Trygonometria Olcia: Jak mam obliczyć cos36'?

kinder: Tablice trygonometryczne

Gray: Co to jest 36'? Trzydzieści sześć stopni? Minut? Sekund? Jak masz to obliczyć, ze wzoru Taylora może?

Olcia: stopni

Gray: A wzór Taylora był ostatnio?

Olcia: nie

Gray: No to faktycznie tablice Ci zostają... Albo jakaś maszyna licząc.

PW: Dokładna wartość jest do policzenia, trzeba jakoś kombinować z wzorami trygonometrycznymi: 36 = 2·18 i 90 = 2·36 + 18 albo może z trójkątem równoramiennym o kącie 72° przy podstawie.

Mila: Pięciokąt foremny i złoty podział.

Olcia: eee... hehe, pierwszy raz widzę takie rozłożenie cosinusa że cos36=cos2*18

PW: Olcia, a czy ja coś takiego napisałem?

Olcia: eh w szkole się jutro popytam, może jakimś magicznym sposobem to zrobili dziękuję za pomoc.

Olcia: no napisałeś że 36=2*18

PW: Zresztą to jest prawda (być może do tego zadania mało przydatna): cos36° = cos(2·18°). A dlaczego piszesz hehe, to ja hehe nie rozumiem, rozumiem ze hehe nie zrozumiałaś.

PW: Postaraj się zrozumieć co napisała Mila, to jest dobry sposób (już na tym forum było to zadanie).

Olcia: nom xD Nie zrozumiałam co z tym bym miała zrobiić dalej.

Olcia: oki Dziękuję

PW: Sposób z trójkątem jest rozwiązany tutaj: 159268

mati89: w książce masz na końcu książki przybliżoną wartość funkcji trygonometrycznych

PW: mati, w tym zadaniu trzeba policzyć wartość dokładną, jest ona równa

	√5 + 1
	4

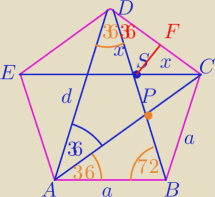
Mila: ABCDE− pięciokąt foremny ΔSCB−Δrównoramienny o kątach: 36^o,72^o,72^o⇔|SB|=a ΔDCS− Δrównoramienny o katach: 36^o,36^o,108^o ΔSCB∼ΔABD⇔

x+a		a
	=		⇔
a		SC

x+a		a
	=		⇔
a		x

x²+ax−a²=0, x>0 Δ=5a²

	−a+a√5
x=
	2

	√5−1
x=		*a
	2

W ΔDSC:

	0,5a		2
cos(36o)=		=0,5a*
	x		a(√5−1)

	1
cos(36o)=
	√5−1

	√5+1
cos(36o)=
	4

================

Eta: Inny sposób( wykorzystam trygonometrię) cos36^o= sin54^o = sin(3*18^o) zamiast α piszę "a" ze wzorów sin(3a)= 3sina −4sin²a i cos(2a)=1−2sin²a to: 1−2sin²18^o=3sin18^o−4sin²18^o , sin18^o=t ,t∊(0,1/2) 4t³−2t²−3t+1=0 W(1)=0 (t−1)(4t²+2t−1)=0 t= 1 −−− odrzucamy i Δ= 2√5

	−1−√5		−1+√5
t=		−− odrzucamy lub t=
	4		4

	√5−1
przy okazji mamy dokładną wartość sin18o=
	4

	6−2√3		3−√5		√5+1
to cos36o =1−2sin218o= 1−2*		= 1−		=
	16		4		4

Eta: No i zapomniałam podkreślić ======================

Mila: Jeszcze jakiś mam algebraiczny, ale nie widzę zainteresowania, to nie piszę.

PW: No, a Olcia wątpiła. Piękne rozwiązanie, ale "=============" to patent Janka191.

PW: Mila, ale bardzo dobrze się bawimy

Eta: Nawet bardzo dobrze ================= =========== ====================

Mila: Pozdrowienia Dobry humor to zdrowie.

Gray:

Kacper: Bardzo ładnie