Zadanie dla znudzonych :P ICSP: Oblicz dokładną wartość sin72^o

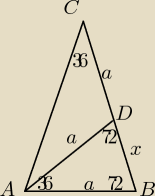
Andrzej: To można policzyć np. z takiego trójkąta: Równoramienny, o kącie między ramionami 36 stopni. Podstawę oznaczamy jako a. Teraz rysujemy dwusieczną kąta A. Z równoramienności widzimy że są jeszcze dwa odcinki równe a. Trójkąty ABC i DBA są podobne na mocy cechy kk. więc

a+x		a
	=		i stąd liczymy x(a).
a		x

i teraz w trójkącie ABD można np. walnąć twierdzenie cosinusów, z którego wyliczymy cos 72 stopni (a się skróci), i dalej z jedynki trygonometrycznej sin 72 stopni. albo z Pitagorasa policzyć wysokość któregoś z trójkątów i dzięki niej tego szukanego sinusa.

ICSP: fajny sposób

Eta: Kiedyś podawałam ten sposób

ICSP: Jeśli się nie mylę Eta to kiedyś dałaś podobne zadanko właśnie z podobnym katem : 20^o

Trivial: 72*5 = 360, co budzi pewne podejrzenia. sin(5x) = sin(4x+x) = sin(x)cos(4x) + cos(x)sin(4x) cos(4x) = cos(2*2x) = 1 − 2sin²(2x) = 1 − 2*(2sinxcosx)² = 1 − 8sin²x(1−sin²x) sin(4x) = 2sin(2x)cos(2x) = 4sinxcosx*(1−2sin²x) sin(5x) = sinx*(1 − 8sin²x(1−sin²x)) + 4sinxcos²x*(1−2sin²x) = sinx*(1 − 8sin²x(1−sin²x)) + 4sinx(1−sin²x)*(1−2sin²x) Podstawiamy u = sinx i mamy: sin(5x) = u(1 − 8u²(1−u²)) + 4u(1−u²)(1−2u²) = u(1 − 8u² + 8u⁴ + 4 − 12u² + 8u⁴) = u(5 − 20u² + 16u⁴) Zatem sin(5x) = sinx*(5 − 20sin²x + 16sin⁴x). Dla x = 72^o mamy: sin(360^o) = sin(72^o)*(5 − 20sin²(72^o) + 16sin⁴(72^o)) Podstawmy s = sin(72^o). s ≠ 0. 0 = s*(5 − 20s² + 16s⁴) 16s⁴ − 20s² + 5 = 0 Δ = 400 − 320 = 80 √Δ = 4√5

	20 ± 4√5		5 ± √5
s2 =		=
	32		8

	5 ± √5
s = √
	8

	5 + √5
Wybieramy odpowiednie rozwiązanie, którym niewątpliwie jest √
	8

ICSP: oo rozwiązanie algebraiczne To lubię Musze przeanalizować

Mila: Możesz obliczyć z pięciokąta foremnego, korzystając ze złotego podziału.... Będziesz miał wartość dokładną. Z Andrzeja sposobu też.