Gemometria analityczna :) Pakri : prosta o równaniu x−y+1=0 jest symetralną odcinka AB o końcach : 1) A=(5,6) i B=(−3,−3) 2) A=(4,1) i B=(−2,5) 3) A=(4,−1) i B=(−2,5)

Pakri : wiemy, że symetralna to prosta prostopadła do danego odcinka i przechodzaca przez jego srodek. wiemy też, że rownanie tej prostej to y=x+1

Pakri :

	1
czyli ten prostopadły odcinek bedzie miał rownanie y=−		+1
	x

Pakri :

	1
zaczy sie −		+ b
	x

Pakri : ale co dalej? bo jakoś nwm co dokłądnie tutaj zrobic

o nie: najprościej sprawdzić, czy środek któregoś z odcinków należy do prostej. https://matematykaszkolna.pl/strona/1750.html jeżeli więcej niż jedna, to trzeba wyznaczyć równania prostych dla odcinków i sprawdzić która jest prostopadła, porównując współczynniki kierunkowe

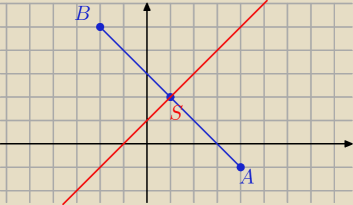
Mila: k: y=x+1 x−y+1=0, u^→[1,−1] wektor prostopadły do prostej k środki odcinków:

	5−3		6−3		3
1)(		,		)=(1,		)
	2		2		2

	3
y=1+1=2≠		⇔prosta nie przechodzi przez środek AB, nie jest sym.
	2

2) S=(1,3)

	3
y=1+1=2≠		⇔prosta nie przechodzi przez środek AB, nie jest sym.
	2

3) S=(1,2) y=1+1=2 prosta przechodzi przez środek odcinka AB⇔prosta k może być symetralną. Sprawdzamy czy jest prostopadła do AB: (a₁*a₂=−1) Prosta AB: y=ax+b −1=4a+b 5=−2a+b ====== −6=6a a=−1 (−1)*1=−1 proste są prostopadłe ⇔ k: y=x+1 jest symetralną odcinka AB, gdzie A=(4,−1) i B=(−2,5)

Pakri : dziękuje już wiem o co chodzi

Mila: