zespolone równanie
Kaktus:
z
6+64=0
(z
2)
3+4
3=0
(z
2+4)(z
4−4z
2+16)
z
2−4i
2=0
(z−2i)(z+2i)=0
z=2i lub z=−2i
z
4−4z
2+16=0
t=z
2
t
2+4t+16=0
Δ=48i
2
√Δ=4
√3i
Wracam do podstawianie
z
2=2−2
√3i
x
2+2xy−y
2=2+2
√3i
x
2−y
2=2
2xy=2
√3
x
2−y
2=2
xy=
√3
x
2+y
2=
√22+(2√3)2
2x
2=6
x
2=3
x=
√3 lub x=−p{3
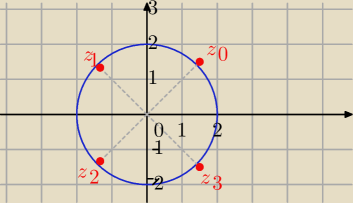
z
1=
√3+i
z
2=−
√3−i
z
2=2−2
√3i
x
2+2xyi−y
2=2−2
√3i
x
2−y
2=2
2xy=−2
√3i
x
2+y
2=
√22+(2√3)2
2x
2=6
x
2=3
x=
√3 lub x=−
√3
z
3=
√3−i
z
4=−
√3+i
Wolfram pokazuję inaczej, więc gdzie robię błąd
15 lis 13:00
bezendu:
Odpowiedzi są dobre
15 lis 13:11
razor: można też inaczej
z
6+64 = 0
z
6−64i
6 = 0
(z
3−8i
3)(z
3+8i
3) = 0
(z−2i)(z
2+2zi−4)(z+2i)(z
2−2zi−4) = 0
z = 2i lub z = −2i lub Δ = ... − dokończ
15 lis 13:15
Kaktus:
A odp dobre ?
15 lis 13:34
Kaktus:
razor masz może czas ?
Chodzi mi o zespolone
15 lis 13:42
xd: dobre dobre
15 lis 13:42
razor: to pisz o co chodzi
15 lis 13:51
Kaktus:
Porównując cześć rzeczywistą i urojoną obu stron rownań znaleźć ich rozwiązania
ź=(2−i)z
x−yi=2z−zi
x−yi=2x+2yi−xi+y
x=2x+y y=−x
−y=2y+x
4x=0
x=0
to ile y ?
15 lis 13:56
Kaktus: ?
15 lis 14:17
Kaktus:
smutna buźka
15 lis 14:40
Kaktus: halo
15 lis 15:00
Kaktus: .
15 lis 16:08
Mila:
y=−x⇒y=0
15 lis 16:23
Kaktus:
czyli z=0 ?
15 lis 18:11
Mila:
Tak.
15 lis 18:14
Kaktus:
A mogę jeszcze prosić o pomoc. ?
15 lis 18:18
Mila:
Jestem, będę umiała, to pomogę.
Pisz.
15 lis 18:22
Kaktus:
wyznaczyć i narysować na płaszczyźnie zespolonej elemnty pierwiastka
4√−16
tutaj chyba nie trzeba liczyć wszystkich pierwiastków tylko wystarczy 2 bo dwa pozostałe będą
symetryczne tak ?
15 lis 18:40
15 lis 18:44
Kaktus:
No ale ja właśnie tego nie rozumiem.
15 lis 19:00
Mila:
To licz z0.
15 lis 19:01
Mila:
1) Narysować okrąg o promieniu :
r=4√|z| ⇔r=4√16⇔
r=2
2) Obliczyć i zaznaczyć jeden pierwiastek z danej liczby , a następnie podzielić okrąg na 4
równe części tak, aby obliczony pierwiastek był jednym z punktów podziału. W ten sposób
otrzymujemy wszystkie pierwiastki z danej liczby .
15 lis 19:07
Kaktus:
z0=16(cosπ+isinπ)
15 lis 19:21
Mila:
Jaki jest wzór na pierwiastek czwartego stopnia?
| | π+2kπ | | π+2kπ | |
zk=4√16*(cos |
| +i sin |
| ) gdzie k=0,1,2,3 |
| | 4 | | 4 | |
dla k=0
oblicz
15 lis 19:32
Kaktus:
Nie ma, już liczę.
15 lis 19:42
Kaktus:
A mogę wiedzieć skąd ten wzór ?
15 lis 19:46
Mila:
Na wykłady chodzisz?
Twierdzenie
Niech z = |z|(cosφ + i sinφ) będzie liczbą zespoloną różną od zera.
Wówczas pierwiastkami stopnia n z liczby z są liczby:
| | φ+2kπ | | φ+2kπ | |
zk=n√|z|*(cos |
| +i sin |
| ) dla k=0,1,2,3,..(n−1), |
| | n | | n | |
===========================================
15 lis 19:56
Kaktus:
Chodzę ale dopiero mieliśmy potęgowanie i proste rachunki na liczbach zespolonych
15 lis 19:57
Kaktus:
moduł 4√−16=16
Może ktoś mi pokazać dla k=0 ?
15 lis 20:14
Mila:
To może za wcześnie rozwiązujesz te zadania?
Teraz policzysz z0?
15 lis 20:15
Mila:
|−16|=16
| | π | | π | |
z0=4√16*(cos( |
| )+i sin( |
| ) |
| | 4 | | 4 | |
z
0=
√2+i
√2
Teraz na kole.
15 lis 20:20
Kaktus:
Nie za wcześnie, u nas na ćw prowadzący wyprzedza wykład i wstawia minusy jak ktoś nie umie
no właśnie dla k=0
| | φ+2*0*π | | φ+2*0*π | |
zk=16(cos |
| +isin |
| ) |
| | 4 | | 4 | |
z
k=16(cos0+isin0)
z
k=16(1+0)
z
k=16
15 lis 20:23
Mila:
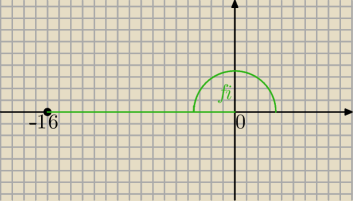
Przecież φ określasz dla liczby (−16)
φ=π
źle , przeczytaj dobrze wzór i moje obliczenia 20:20.
15 lis 20:31
Kaktus:
Dobrze poczytam i spróbuję jeszcze raz
15 lis 20:34
Kaktus:
20:23 gdzie jest błąd ?
15 lis 21:34
Mila:
4√16 czyli 2 zamiast 16
15 lis 21:46
Kaktus:
ale moduł z 4√−16=16
i czemu nie zero skoro podstawiając za k=0 to się zeruję ?
15 lis 21:48
Mila:
Nie liczysz modułu z
4√−16 bo nie wiesz ile to jest, ale liczysz moduł z liczby pod
pierwiastkiem,
czyli z (−16).
1) z=−16
|z|=16 wyciągasz z tego pierwiastek 4 −tego stopnia
2) masz we wzorze :
| | π+2*0*π | | π+0 | | π | |
cos( |
| )=cos |
| =cos |
| |
| | 4 | | 4 | | 4 | |
15 lis 21:56
Kaktus:
Ok już jaśniej się robi
15 lis 22:09