elipsa raf.36: https://matematykaszkolna.pl/forum/229733.html Interesuje mnie zadanie 6. Dlaczego te same x, y są brane dla pola prostokąta i równania elipsy?

Janek191: Mamy

	y2
b2 x2 + a2 y2 = a2 b2 ⇔ U{x2}[a2} +		= 1 − r − nie elipsy
	b2

P = ( x; y) leży na elipsie Pole prostokąta jest równe: P = 2 x*2 y = 4 x*y oraz a² y² = a²b² − b² x²

	b2		x2
y2 = b2 −		x2 = b2*( 1 −		)
	a2		a2

	x2
y = b √ 1 −
	a2

	b
y =		√a2 − x2
	a

więc

	b		b
P = 4x*		√a2 − x2 =		*√ 16x2*(a2 − x2)
	a		a

P( x) będzie największe, gdy 16x²*(a² − x²) będzie największe. Niech f(x) = 16 x²*( a² − x²) ; więc f '(x) = 32x*(a² − x²) + 16 x²*( −2x) = 32 a² x − 32 x³ − 32 x³ =

	a
= 32x *( a2 − 2 x2) = 0 ⇔ x =
	√2

	a
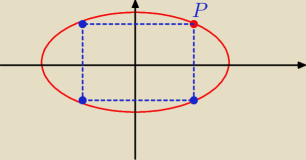
Łatwo zauważyć, że dla x =		funkcja f osiąga maksimum, czyli pole P
	√2

jest największe. oraz

b

b

a2

b

a

b

y =

*√a2 − x2 =

*√a2 −

=

*

=

a

a

2

a

√2

√2

Pole P jest zatem równe

	a		b
Pmax = 4x*y = 4*		*		= 2a*b
	√2		√2

raf.36: Dziękuję.