pochodne w zadaniach studia krysicki Alois~: Trochę tego jest wieem.. ale nie mam pojęcia nawet jak się zabrać do niektórych , no poza rysunkami które niewiele dają. Nie posiadam podobnych przykładów żeby na czymś się wzorować niestety. podaje też odpowiedzi z książki Bardzo bardzo proszę o pomoc. 1. W daną kule o promieniu r wpisano prawidłowy ostrosłup czworokątny . Zbadać przebieg zmienności V tego ostrosłupa.

	64
odpowiedz Vmax =		r3 krawędź 4/3 r
	81

2. Na kuli o danym promieniu r opisano stożek obrotowy. Zbadać przebieg zmienności V tego stożka. Odp minimalna objętość stożka równa się podwojonej objętości kuli 3. Zbadać przebieg zmienności V walca wpisanego w kulę o promieniu R.

	4
odp		πR3 √3
	9

4.Zbadać przebieg zmienności powierzchni bocznej walca wpisanego w kule o promieniu R. odp 2 πR² 5. W dane koło o promieniu r wpisano trójkąt równoramienny. Zbadać przebieg zmienności pola S trójkąta odp 3/4 r² √3 6.w elipsę b²x² +a²y² = a²b² wpisano prostokąt o bokach równoległych do osi elipsy. zbadać przebieg zmienności pola S tego prostokąta odp Smax=2ab prostokat o bokach a√2 i b√2 7. w daną półkulę o promieniu r wpisano stożek , którego wierzchołek leży w środku kuli , a podstawa jest równoległa do podstawy półkuli. zbadać przebieg zmienności V tego stożka.

	2
odp		πr3√3
	27

Alois~: nawet same zależności , które potem bedzie trzeba podstawic do samego wzoru ostatecznego bardzo by mi pomogły, cokolwiek to może by mi coś wyszło

Alois~:

Alois~: proosze

Maslanek: Jeśli zbadać przebieg zmienności, to podać wzór jak to się zmienia? I czy w odpowiedziach jest ten wzór, czy maksimum/minimum?

Maslanek: Jak spróbowałem elipsę zrobić dla wyzwania, to wyszła kicha, bo nie wiem jak to działa xD (chciałem wrzucić jakiegoś Talesa, ale to nie ma prawa wyjść tak jak ja chciałbym to zrobić ). Jeśli chodzi o 5, które wydaje się proste, to rysuję sobie trójkąt i zaznaczam kąt przy równych ramionach jako 2α. Od centrum do wszystkich wierzchołków mamy odległość R, więc łatwo jest nam policzyć pole trójkąta jako sumę trzech małych trójkątów.

	1		1
Wtedy P=2*(		r2*sin(π−2α))+		r2*sin(π−2*(π−2α))
	2		2

	dP		dP
Liczymy		, przyrównujemy do zera i dostajemy, że		=0 ⇔ 2cos2α+2cos4α=0
	dα		dα

Wzór na sumę cosinusów daje nam równanie cos3α*cos(−α)=0, które rozwiązać jest już prosto.

Alois~: wypisac zaeznosci te równania i wstawic do jednego wzoru uzaleznione od jednej zmiennej i pochodna i potem zbadac kiedy jest najwieksze ja wlasnie tez nie wiem jak dziala elipsa po zrobieniu rysunku i zobaczeniu wzoru w tablicach ( co nic mi nie dalo) sie poddalam. Jutro bede cos kombinowac z reszta zadan..

Alois~: i dzięki za 5 rano je ogarne

RS: Alois co studiujesz ?

Alois~: budownictwo

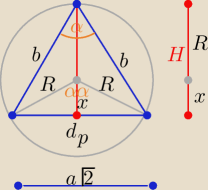
Eta: zad1/

a√2
	=2R ⇒ a=√2*R*sinα , x= R*cosα , to H= R(1+cosα)
sinα

	2
V(α)=		R3*sin2α*(1+cosα)
	3

	1		2√2
V'(α)= .......... V'(α)=0 ⇒ ...... cosα=		⇒ sinα=
	3		3

V(max)= ......... dokończ

Eta:

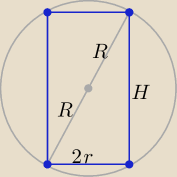
	1
4r2= 4R2−H2 ⇒ r2= R2−		H2
	4

	1		1
V(H)= π (R2−		H2)*H = πR2*H−		π*H3
	4		4

	3		2√3
V"(H)= πR2−		πH2 to V'(H)=0 ⇒ .......... H=		*R
	4		2

r²=.......... V{max) =...... dokończ i otrzymasz właściwą odp ( którą podajesz Powodzenia w następnych zadaniach ( bo ja na chwilę wychodzę z

Eta: No i...... wypadałoby z przyzwoitości napisać słowo (dziękuję

Alois~: już liczę dziękuję bardzo Eta !

	R*sinα
tam chyba będzie w pierwszym tylko a=		o ile dobrze poprawiam ?
	√2

Alois~:

	2R3
do 1 pochodna mi wyszła		* (sinα(2cosα+3cos2α−1)
	3

Eta:

	2Rsinα		2√2Rsinα
1/ a=		=		= √2Rsinα i tak jest !
	√2		2

Alois~: czyli (sinα(2cosα+3cos²α−1) =0 t=cosα sinα=0 dla α=0 3t²+2t−1=0 Δ=16 t₁ = 1/3 dla α = ...? t₂ = 1 dla α=0

Alois~: juz doszlam do tych 2√3 /3

Eta: sinα=0 −− nie spełnia warunku zadania ( dlaczego? 3cos²α+2cosα−1=0 Δ=16 √Δ=4

	1
cosα=		v cosα= −1 −−− nie spełnia warunków zad.
	3

	1
i teraz jeżeli cosα=		to: sinα=...
	3

I V(max)=..... dokończ te proste już rachunki

Alois~: wyszło jak w odpowiedziach bardzo dziękuje, robię dalej !

Alois~: 3 też wyszło postaram się resztę coś sama pokombinować ewentualnie wstawię tylko tego z elipsą na pewno nie zrobię

Alois~: 4 też wyszło czyli 1,3,4 już mam

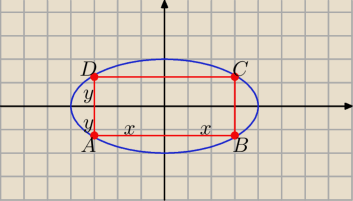
Eta: zad 6/ x∊(0,a) , y∊(0,b) P(ABCD)= 2x*2y=4xy

	b		b
bx2+ay2=a2b2 ⇒ y2=(		)2*(a2−x2) ⇒ y=		*√a2−x2
	a		a

	b
P(x)= 4x*		*√a2−x2
	a

	4b		4bx2		1
P'(x) =		*√a2−x2−		*
	a		a		√a2−x2

	x2
P'(x)=0 ⇒ √a2−x2 −		=0 ⇒a2−x2−x2=0 /*2
	√a2−x2

to 4x²= 2a² ⇒ 2x= √2*a i 2y=.......... = √2b P_max = √2a*√2b= 2ab

Eta:

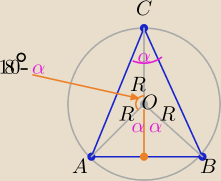
	1		1
P(ABC)= 2p(AOC)+P(ABO) , P(AOC)=		R2*sinα , P(ABO)=		R2*sin2α
	2		2

P(α)= R²sinα+0,5R²sin2α = R²(sinα+0,5sin2α) P^'(α)=........... i dokończ

Alois~: Eta bardzo dziękuję mam 2 ale gdzieś się machnęłam i nie mogę znaleźć ( już przepisuję )

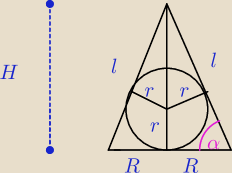
Alois~: P=1/2H 2R=HR 2* 1/2 rl + 1/2 r 2R =P P= rl + rR

H
	=sinα H= l sinα
l

R
	=cosα R=lcosα
l

	P
r=
	l+R

r (l+R) = HR r (l+lcosα)= l² sinα cosα

	r(1+cosα
l=
	cosαsinα

V=1/3 R² Hπ

	r3(1+cosα)3
V=1/3
	(cosαsin2α)

V' = 1/3 r³[−3(1+cosα)² (cosα−cos³α)−(1+cosα)³(−1+3cos²α) (1+cosα)²(−2cosα−3cos²α+1)=0 cosα=−1 v cosα=1/3 wyliczyłam sinα i podstawiłam do wzoru na V

r3		43 3		16
			π..=		r3π
3		1/3 *8/9		6

czy to jest dobrze?

Alois~: o prosze jak dodałam to już widzę że wyszlo jak w odpowiedzi

Eta: