Kąty w trójkącie ABC Ludwig1234: Cześć, oto treść zadania: W trójkącie ABC kąt przy wierzchołku A ma miarę 60 stopni, a dłuższa przyprostokątna ma długość 6 cm. Długość krótszej przyprostokątnej jest równa: A. 4√3 B. 2√3 C. 12 D. 6√3 Zastosowałem się do zasad: https://matematykaszkolna.pl/strona/2280.html i wychodzi mi 2√3. Odpowiedź poprawna brzmi 6√3. O dziwo autorzy wykorzystują trygonometrię, co znacznie utrudnia sprawę. Coś źle obliczyłem? Poproszę o jakieś sugestie.

Metis:

	a
tgα=
	6

	a
√3=
	6

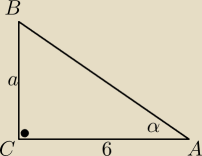
a=6√3 ... Poza tym "autorzy wykorzystują trygonometrię, co znacznie utrudnia sprawę" a to w tym linku co podałeś to myślisz z jakich zależności jest zaczerpnięte...

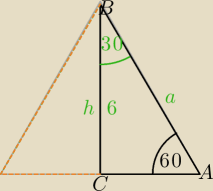
Mila: Jeśli korzystasz z własności Δ o katach 30,60, 90, to dorysuj sobie Δ, aby mieć Δ równoboczny wtedy nie pomylisz się. Dłuższa przyprostokątna leży naprzeciw kąta o mierze 60^o. ⇔ jest wysokością Δ równobocznego o boku a

a√3
	=6 /*2
2

a√3=12 /*√3 a*3= 12√3 /:3 a=4√3 |AC|=2√3 ====== spr.

	4√3*√3		12
h=		=		=6
	2		2

Metis: Milu Ale mój zapis jest w porządku

Mila: Metis, jeżeli dłuższa przyprostokątna ma długość 6, to leży naprzeciw kata 60^o. Rysunek błędnie oznaczony. Nie wiem, dlaczego tak odpowiedź podana .

Ludwig1234: Wychodzi właśnie 6√3. Muszę to zrobić trygonometrią, aby wynik był poprawny? Nie da rady inaczej?

Mila: Co to znaczy wychodzi? Zobacz, czy treść dobrze przepisana?

Ludwig1234: Dobrze przepisana. 6√3 jest w odpowiedzi, czemu sam się dziwię. Może popełnili pomyłkę? W modelu jest napisane: Krótsza przyprostokątna leży naprzeciwko kąta 60 stopni. Zatem: 6/x = tg30 c = 6/√3/3 x=6√3 To jednak Waszym zdaniem zrobiłem na początku dobrze? Już się pogubiłem, szczerze mówiąc.

Metis: Oczywiście Milu masz rację Najwidoczniej autorzy założyli błędnie− tak jak ja.

Mila: Ludwik, z jakiej to książki?

Ludwig1234: Repetytorium maturalne 2015 z Operonu, zakres podstawowy. Dzięki za wytłumaczenia.