zespolone
Radek:
Na płaszczyźnie zespolonej narysować ?
Re(z−i)2≥0
Re(z2−2zi−1)≥0
Re[(x+yi)−2zi−1)]≥0
Re(x2+2xyi−y2−2zi−1)≥0
Re(x2−y2−1)+(2xy−2z)i≥0
x2−y2−1≥0
?
18 paź 18:21
ICSP: źle. Dlaczego za z nie podstawi x + yi ?
18 paź 18:24
Radek:
bo z=(x+yi)
18 paź 18:26
Radek:
dobra już wiem.
18 paź 18:27
Radek:
Re(x2−y2+2y−1)+(2xy−2x)i≥0
x2−y2+2y−1≥0
x2−(y2−2y+1)≥0
|x|−|y−1|≥0
18 paź 18:29
Mila:
Nie możesz zostawić liczby z w części Im.
z=x+iy, x,y∊R
(z−i)2=(x+iy−i)2=[x+i(y−1)]2=
=x2+2x(y−1)i+(y−1)2*i2=
Re(z−i)2=x2−(y−1)2
x2−(y−1)2≥0⇔
(x−(y−1))*(x+(y−1))≥0
dokończ
18 paź 18:32
Radek:
już mam |x|−|y−1|≥0
|x|≥|y−1|
ale jak to naszkicować w układzie ?
18 paź 18:33
ICSP: Przedziały.
1o x ≥ 0 i y ≥ 1
2o x < 0 i y ≥ 1
3o ...
4o ...
18 paź 18:35
Mila:
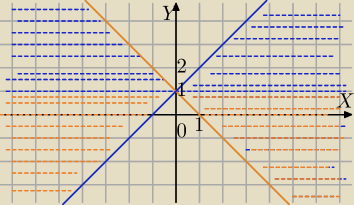
Trzeba rozważać w przedziałach .
|x|≥|y−1|⇔
|y−1|=y−1 dla y≥1
1) y−1≤|x|⇔y≤|x|+1 i y≥1 punkty powyżej prostej y=1 i poniżej wykresu y=|x|+1
2) |y−1|=−y+1 dla y poniżej prostej y=1
|x|≥−y+1
y≥−|x|+1
II sposób
Z wersji : (x−(y−1))*(x+(y−1))≥0⇔(x−y+1)*(x+y−1)≥0
Mamy:
[x−y+1≥0 i x+y−1≥0 ] lub [ (x−y+1)≤0 i (x+y−1)≤0]
[y≤x+1 i y≥−x+1] lub [y≥x+1 i y≤−x+1]
18 paź 18:52
Radek:
Czyli jak rozpisałem w przedziałach to mam tak ?
1 x≥0 y−1≥0
y≤x+1
2 x≥0 y−1<0
y≥−x+1
3. x<0 y−1<0
y≥x+1
4. x<0 y−1≥0
y≥−x+1
18 paź 19:18
Radek:
Robiąc na przedziały cały czas wychodzi źle..
18 paź 19:36
Mila:
18:52 masz przedziały, tylko do |y−1| i wystarczy, przeczytaj uważnie.
Nie ma potrzeby tak komplikować.
II sposób ma tę zaletę, że unkikasz takiego rozpisywania.
Nie upieraj się przy najtrudniejszym sposobie, bo łatwo się pomylić.
19:18
4) punkt powinien być :
x<0 i y−1≥0
−x≥y−1
−x+1≥y
y≤−x+1
18 paź 20:18
Radek:
Ale ten sposób jest dla mnie najłatwiejszy..
18 paź 20:19
Mila:
W takim razie ,źle interpretujesz warunki, skoro Ci nie wychodzi.
Może rysuj po kolei, to powiem, gdzie masz błąd.
18 paź 20:29
Radek:
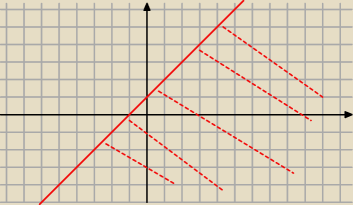
y≤x+1
18 paź 20:31
Radek:
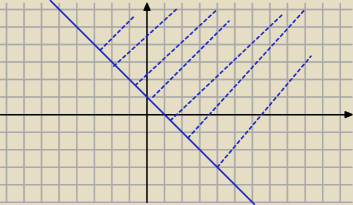
2. y≥−x+1
18 paź 20:32
Radek:
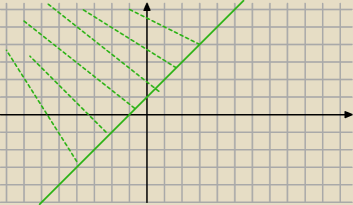
y≥x+1
18 paź 20:33
Radek:
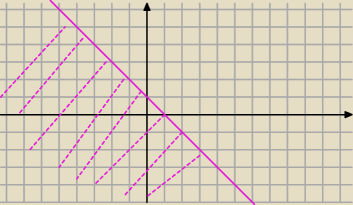
y≤−x+1
18 paź 20:35
Mila:
Czerwony obszar ma być tylko dla x≥0
Niebieski obszar tylko dla x≥0
18 paź 20:35
Radek:
No właśnie czyli to jeszcze trzeba ograniczać.
18 paź 20:37
Mila:
Zielony obszar tylko dla x<0
Różowy obszar tylko dla x<0
Potem części wspólne (1) i (2) oraz (3 i 4) i wszystko będzie dobrze.
18 paź 20:38
Radek:
dziękuję, pomyślę jeszcze nad tym innym rozwiązaniem
18 paź 20:42
Mila:
Już Ci wyszło dobre rozwiązanie?
18 paź 20:43
Radek: Tak.
18 paź 20:56
Mila: Dobrze

18 paź 21:03
Radek:
Mogę jeszcze prosić o wyjaśnienie tego pierwszego sposobu ?
18 paź 21:16
Mila:
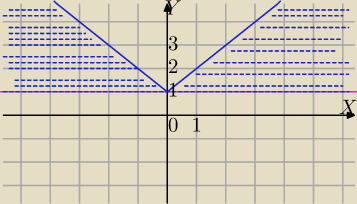
|x|≥|y−1|⇔
1) |y−1|=
df y−1 dla y≥1 czyli punkty nad prostą y=1
wtedy mamy równanie:
|x|≥y−1⇔y≤|x|+1 i y≥1 punkty powyżej prostej y=1 i poniżej wykresu y=|x|+1
Już rysuje tylko ten przypadek:
18 paź 21:24
Radek:
W sumie mnie rysowania, ale trzeba wiedzieć które przypadki wybrać a które odrzucić.
18 paź 21:39
18 paź 22:00
 Trzeba rozważać w przedziałach .
|x|≥|y−1|⇔
|y−1|=y−1 dla y≥1
1) y−1≤|x|⇔y≤|x|+1 i y≥1 punkty powyżej prostej y=1 i poniżej wykresu y=|x|+1
2) |y−1|=−y+1 dla y poniżej prostej y=1
|x|≥−y+1
y≥−|x|+1
II sposób
Z wersji : (x−(y−1))*(x+(y−1))≥0⇔(x−y+1)*(x+y−1)≥0
Mamy:
[x−y+1≥0 i x+y−1≥0 ] lub [ (x−y+1)≤0 i (x+y−1)≤0]
[y≤x+1 i y≥−x+1] lub [y≥x+1 i y≤−x+1]
Trzeba rozważać w przedziałach .
|x|≥|y−1|⇔
|y−1|=y−1 dla y≥1
1) y−1≤|x|⇔y≤|x|+1 i y≥1 punkty powyżej prostej y=1 i poniżej wykresu y=|x|+1
2) |y−1|=−y+1 dla y poniżej prostej y=1
|x|≥−y+1
y≥−|x|+1
II sposób
Z wersji : (x−(y−1))*(x+(y−1))≥0⇔(x−y+1)*(x+y−1)≥0
Mamy:
[x−y+1≥0 i x+y−1≥0 ] lub [ (x−y+1)≤0 i (x+y−1)≤0]
[y≤x+1 i y≥−x+1] lub [y≥x+1 i y≤−x+1]
 y≤x+1
y≤x+1
 2. y≥−x+1
2. y≥−x+1
 y≥x+1
y≥x+1
 y≤−x+1
y≤−x+1

 |x|≥|y−1|⇔
1) |y−1|=df y−1 dla y≥1 czyli punkty nad prostą y=1
wtedy mamy równanie:
|x|≥y−1⇔y≤|x|+1 i y≥1 punkty powyżej prostej y=1 i poniżej wykresu y=|x|+1
Już rysuje tylko ten przypadek:
|x|≥|y−1|⇔
1) |y−1|=df y−1 dla y≥1 czyli punkty nad prostą y=1
wtedy mamy równanie:
|x|≥y−1⇔y≤|x|+1 i y≥1 punkty powyżej prostej y=1 i poniżej wykresu y=|x|+1
Już rysuje tylko ten przypadek: