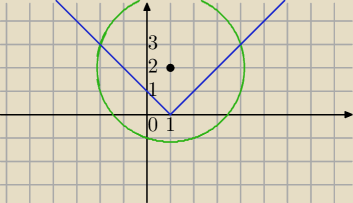
ukł. równań drugiego stopnia Code::Blak: Rozwiąż układ równań i podaj jego interpretacje geometryczną ( nie musicie ) d) { y = |x−1| x² + y² − 2x − 4y − 5 =0 } Wychodzi mi coś takiego x² − 2x + 1 + |x−1|² − 4|x−1| + 4 = 10 (ale możecie jeszcze raz policzyć ) Ok i co dalej z tym zrobić ?

Mila: (x−1)²+(y−2)²=10 postać kanoniczna równania danego okręgu y=|x−1| (x−1)²+(|x−1|−2)²=10 1) |x−1|=x−1 dla x≥1 wtedy masz równanie (x−1)²+(x−3)²=10 stąd x=0∉D lub x=4 x=4 y=3 ==== 2) |x−1|=−x+1 wtedy masz równanie: (x−1)²+(−x−1)²=10 stąd x=2 ∉D lub x=−2 x=−2 y=3 ===

Code::Blak: (x−3)² to skąd opuściłaś wartość bezwzględną ?

Code::Blak: a raczej czy tak można

Code::Blak: 2) |x−1|=−x+1 wtedy masz równanie: // chwila jak ? (x−1)2+(−x−1)2=10 stąd x=2 ∉D lub x=−2 x=−2 y=3 ===

Mila: 2)x<1 (x−1)²+(−x+1−2)²=10⇔ (x−1)²+(−x−1)²=10⇔ (x−1)²+(x+1)²=10 x²−2x+1+x²+2x+1=10 2x²=8 x²=4 x=2∉(−∞,1) lub x=−2 Coś się nie zgadza?

Code::Blak: po prostu się zdziwiłem i tyle

Mila: A co Cię zdziwiło?

Code::Blak: no że tak można postąpić z wartością bezwzględną

Code::Blak: https://matematykaszkolna.pl/forum/261219.html

Mila: Wartość b. podstawiamy tylko za y. Przeczytaj dokładnie co napisałam.