Uk. rów. drugiego stopnia Code::Blak: W okręgu o równaniu (x − 2 )² + y² = 25 wpisano kwadrat. Wyznacz współrzędne wierzchołków tego kwadratu, jeśli : a) jedna z jego przekątnych jest zawarta w prostej 4x − 3y = 8 b) jeden z jego boków jest zawarty w prostej y = 3+x

Mila: Napisz swoją koncepcję.

Code::Blak: Tak. Mając informacje o przekątnej (prostej) czyli ona leży na prostej 4x−3y=8 −3y= 8 − 4x | *(−1) 3y=4x − 8 | /3 y= 4/3x − 8/3 mam punk S o współrzędnej ( 2 , 0 ) r= 5 Obliczam długość |AS|= 5 czyli 5 = √ (2 − x)² + (4/3x + 8/3) ² | ()² 25 = (2 − x)² + ≠(4/3x + 8/3) ² // i teraz mnie to strachem napawa szczególnie ten drugi nawias

Code::Blak: zapawne zły pomysł ale na lepszy nie wpadłem

Mila: Za pół godziny będę.

Code::Blak: :C

Mila: Właśnie coś sobie przycisnęłam i wszystko zniknęło. bezendu, Piotr jak to odzyskać?

Code::Blak: ctrl + z ?

Code::Blak: udało mi się jeden wierzchołek obliczyć

Eta: Drugi raz pisać Pozdrawiam

Code::Blak: to może ja skorzystam i pokaże jak obliczyłem wierzchołek D ?

Code::Blak: a nie wróć to inne zadanie

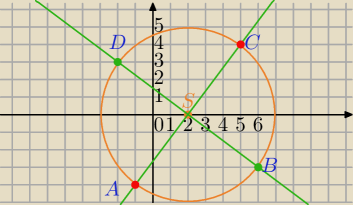Mila: Rozwiązuję układ równań: okrąg (x − 2 )² + y² = 25

	4		8		4
prosta AC: y=		x−		⇔y=		*(x−2) (łatwiejsza postać do podniesienia do kwadratu)
	3		3		3

	4
y2=(		)2*(x−2)2
	3

	4
(x−2)2+(		)2*(x−2)2=25
	3

	16
(x−2)2+		*(x−2)2=25
	9

	16
(x−2)2*(1+		)=25
	9

	25		9
(x2−4x+4)*		=25 /*
	9		25

x²−4x+4=9 x²−4x−5=0 Δ=36 x=−1 lub x=5, co widać na rysunku

	4
A=(−1,		*(−1−2))=(−1,−4)
	3

C=(5,4) BD⊥AC BD:

	3
y=−		x+b i S=(2,0) ∊prostej BD
	4

	3
0=−		*2+b
	4

	3
0=−		+b
	2

	3
b=
	2

	3		3
y=−		x+
	4		2

Teraz rozwiąż układ równań: okrąg (x − 2 )² + y² = 25

	3		3
Prosta BD:y=−		x+
	4		2

	−3
y=		*(x−2)
	4

Mila: Pozdrawiam Eta.

Code::Blak: chwilkę ukł to { (x−2)² + y²= 25 y=−3\4x + 3\2 } tak?

Mila: Przecież napisałam, tak.21:22 − 4 ostatnie linijki.