. Mat: Znajdź współrzędne punktu symetrycznego do A(1,−1) względem prostej x−2y−4=0 Witam. Mam wykres i nie wiem zbytnio co robić dalej.Mogę wyznaczyć równanie prostej przechodzącej przez A A' ale jak znaleźć to A'. Proszę o pomoc.

5-latek: Nie trzeba bylo tak od razu zrobic tylko te wykrzykniki dawac do ogladania ?

daras: prosta AA' jest ⊥ do danej prostej i A' lezy w takiej samej odległosci od niej co A (lustro)

daras: a dalej ..sam

5-latek: Dobry wieczor daras Dam mu post gdzie napisalem jak to rozwiazc zeby to dziadowstwo z tymi wykrzyknikami zeszlo jak najszbciej na dol https://matematykaszkolna.pl/forum/260294.html

Mat: 5 latek to nie ja dawałem te wykrzykniki

5-latek: Ja wiem ze nie Ty ale one mnie denerwuja strasznie czy juz wiesz jak masz rozwiazac ?

Mat: Wyszło mi że y₂=−2x+1 Pytanie1: Czy moge ją nazwać y₂ i podpisać na wykresie że jest to y₂? Pytanie2: Co dalej. Z geometrii analitycznej nie umiem nawet podstaw i chce od czegoś zacząć dlatego nie chce nauczyć się źle dlatego o wszystko pytam.

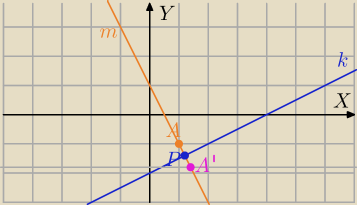
Mila: A=(1,−1) A'(x,y) punkt symetryczny do punktu A względem prostej k, gdzie : k: x−2y−4=0 postać ogólna równania prostej x−4=2y

	1
y=		x−2 postać kierunkowa równania prostej k
	2

Odcinek AA' jest prostopadły do k; m prosta prostopadła do k i A∊m m⊥k y=−2x+b i −1=−2*1+b⇔b=1 m: y=−2x+1 Szukamy punktu przecięcia prostych m i k,

	1
−2x+1=		x−2
	2

	6		6		7
x=		to y=−2*		+1=−
	5		5		5

	6		6
P=(		,		) punkt P jest środkiem AA'.
	5		5

6		1+x		−7		−1+y
	=		i		=		⇔
5		2		5		2

	7		−9
x=		, y=
	5		5

	7		−9
A'=(		,		)
	5		5

================

daras: ciekawe tylko czy Mat poniał ?

AS: Dane: prosta l: x − 2*y − 4 = 0 , punkt A(1,−1) Szukane: punkt B(a,b) symetrycznie położony do A względem prostej l Rozwiązanie Wsp.kierunkowy prostej l: m = 1/2 Wsp.kierunkowy prostej AB: mp = −1/m = −2

	b + 1
czyli		= −2 po uporządkowaniu 2*a + b = 1 [1]
	a − 1

środek odcinka AB: xs = (a + 1)/2 , ys = (b − 1)/2 środek ten należy do prostej l czyli spełnia równanie tej prostej

a + 1		b − 1
	− 2*		− 4 = 0 po uporządkowaniu
2		2

a − 2*b = 5 [2] Rozwiązując układ równań [1] i [2] otrzymujemy a = 7/5 , b = −9/5 Szukany środek: S(7/5,−9/5)

daras: poniał

Mila: Mat na pewno dzisiaj jest na randce, jutro tu spojrzy.

pigor: ..., znajdź współrzędne punktu symetrycznego do A=(1,−1) wzgl.proste x−2y−4=0 . −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− to jeszcze ja "zamieszam" np. tak : [1,−2] − wektor kierunkowy prostej p⊥−łej do danej, czyli prostej (*) p: (x,y)= (1+t,−1−2t) w postaci parametrycznej przez punkt A takiej, że 1+t+2+4t−4= 0 ⇔ 5t=1 ⇔ t=¹₅ , a stąd i z (*) S=(x,y)= (1+¹₅, −1−²₅)= (⁶₅,−⁷₅) − punkt przecięcia p z daną prostą i środek odcinka AA' zatem jeśli A'=(x,y) − obraz punktu A=(1,−1) w symetrii osiowej, to x+1= ¹²₅ i y−1= −¹⁴₅ ⇒ x= ⁷₅ i y= −⁹₅, czyli A'=(⁷₅,−⁹₅) − szukany punkt spełniający warunki zadania . ... .