Rozwiąż
matematyk: |x−2|−|x−1|≥|x+1| −5
PS. Czy mogę to podnieść do kwadratu?
6 paź 10:56
J: Nie ... a poza tym, co Ci to da ?
6 paź 11:07
matematyk: Ktoś mi dał rade żeby tak zrobić, ale mi nie wychodziło dobre rozwiązanie.
6 paź 11:13
J:
... widzę,że często korzystasz z "dobrych rad" ..

6 paź 11:31
PW:
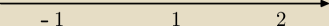
|x+1| + |x−1| − |x−2| − 5 ≤ 0
Zgodnie z definicją wartości bezwzględnej na każdym z tych przedziałów funkcja po lewej stronie
ma inną definicję.
Rozpatrujmy przedział (−
∞,−1), na którym wszystkie wyrażenia między kreseczkami wartości
bezwzględnych są ujemne
−(x+1) + (−(x−1)) − (−(x−2)) − 5 ≤ 0, x∊(−
∞,−1)
− x−1 −x +1 +x − 2 − 5 ≤ 0
− x − 7 ≤ 0
x ≥ − 7.
Na rozpatrywanym przedziale rozwiązaniami są więc x∊[−7, −1).
Rozpatrujemy przedział [−1, 1), na którym nierówność przyjmuje postać
x + 1 − x + 1 + x −2 − 5 ≤ 0, x∊ [−1, 1)
x − 5 ≤ 0
x ≤ 5.
Na rozpatrywanym przedziale rozwiązaniami są wszystkie x∊[−1, 1).
Zostały jeszcze dwa przedziały, powodzenia.
6 paź 11:40
6 paź 11:46
matematyk: Nie to że nie przyjmuje ich do wiadomości, bo to jest sposób którym jak to rozwiązałam, ale jak
zajrzałam do odpowiedzi to był pokazany inny sposób i dlatego napisałam tutaj te zadania bo
kompletnie nie rozumiem dlaczego nie mogę rozwiązać tego tym podstawowym sposobem.
6 paź 11:51
J:
.... a nie bierzesz pod uwagę faktu,że często są pomyłki w rozwiązaniach..

6 paź 12:08
5-latek: Powiem CI ze najlepiej jest rozwiazywaz sposobem ktorym mialas pokazany na lekcji
6 paź 12:16
matematyk: Nie możliwe że jest błąd w tej książce. 5−latek

jakbym miała to na zajęciach to bym jakoś to
tozwiązała, niestety nie mieliśmy tego..

6 paź 17:30
6 paź 17:34
PW: Dziecko, jak już prawie rozwiązałem, to Ty piszesz, że tak, tym sposobem to już rozwiązałaś,
To znana szkoła − zamiast podziękować, to się grymasi, że jednak nie to. Prościej byłoby
zacytować sposób (wskazówkę) z książki i poprosić o wytłumaczenie.. Po co tracimy czas, jeśli
umieszsz rozwiązać?
6 paź 17:58
matematyk: Ja bardzo Ci dziękuje że mi to rozwiązałeś, i nie mam na myśli tego przykładu, bo "J" dodał
linka z innym moim przykładem
6 paź 18:01
PW: Oczywiście z]że można tamto zadanie rozwiązać "tradycyjnym" sposobem − rozpatrując dwie różne
nierówności na dwóch różnych przedziałach.
x−|5x−2|<0
Jest to jednak tak łatwa nierówność, że
możemy pokusić się o rozwiązanie odbiegające od
sztampy "rozbijania na przedziały".
Widać, że nierówność
x < |5x−2|
jest prawdziwa w sposób oczywisty, gdy x < 0 (lewa strona ujemna, prawa nieujemna).
Część rozwiązania już mamy: nierówność jest prawdziwa dla wszystkich x ∊(−
∞,0) .
Dla x ≥ 0 mamy nierówność o obu stronach nieujemnych, po podniesieniu do kwadratu otrzymamy
więc równoważną
x
2 < 25x
2 − 20 x + 4, x ∊[0,
∞).
0 < 24x
2 − 20 x + 4
0 < 6x
2 − 5x + 1
| | 1 | | 1 | |
Δ = 1, x1 = |
| , x2 = |
| . Po uwzględnieniu, że x∊[0,∞).widzimy, że rozwiązaniem są |
| | 3 | | 2 | |
| | 1 | | 1 | |
Odpowiedź: Rozwiązaniami nierówności są x∊R\[ |
| , |
| ] |
| | 3 | | 2 | |
Wcale mnie ten sposób nie zachwyca, zamiast dwóch prostych nierówności liniowych mamy
nierówność kwadratową na ograniczonej dziedzinie (częste błędy).
Jeżeli napiszesz, że tak to ty już rozwiązałaś, a w książce jest inny sposób, co cię ugryzę.
6 paź 18:31

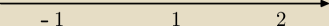 |x+1| + |x−1| − |x−2| − 5 ≤ 0
Zgodnie z definicją wartości bezwzględnej na każdym z tych przedziałów funkcja po lewej stronie
ma inną definicję.
Rozpatrujmy przedział (−∞,−1), na którym wszystkie wyrażenia między kreseczkami wartości
bezwzględnych są ujemne
−(x+1) + (−(x−1)) − (−(x−2)) − 5 ≤ 0, x∊(−∞,−1)
− x−1 −x +1 +x − 2 − 5 ≤ 0
− x − 7 ≤ 0
x ≥ − 7.
Na rozpatrywanym przedziale rozwiązaniami są więc x∊[−7, −1).
Rozpatrujemy przedział [−1, 1), na którym nierówność przyjmuje postać
x + 1 − x + 1 + x −2 − 5 ≤ 0, x∊ [−1, 1)
x − 5 ≤ 0
x ≤ 5.
Na rozpatrywanym przedziale rozwiązaniami są wszystkie x∊[−1, 1).
Zostały jeszcze dwa przedziały, powodzenia.
|x+1| + |x−1| − |x−2| − 5 ≤ 0
Zgodnie z definicją wartości bezwzględnej na każdym z tych przedziałów funkcja po lewej stronie
ma inną definicję.
Rozpatrujmy przedział (−∞,−1), na którym wszystkie wyrażenia między kreseczkami wartości
bezwzględnych są ujemne
−(x+1) + (−(x−1)) − (−(x−2)) − 5 ≤ 0, x∊(−∞,−1)
− x−1 −x +1 +x − 2 − 5 ≤ 0
− x − 7 ≤ 0
x ≥ − 7.
Na rozpatrywanym przedziale rozwiązaniami są więc x∊[−7, −1).
Rozpatrujemy przedział [−1, 1), na którym nierówność przyjmuje postać
x + 1 − x + 1 + x −2 − 5 ≤ 0, x∊ [−1, 1)
x − 5 ≤ 0
x ≤ 5.
Na rozpatrywanym przedziale rozwiązaniami są wszystkie x∊[−1, 1).
Zostały jeszcze dwa przedziały, powodzenia.
 https://matematykaszkolna.pl/forum/259908.html
https://matematykaszkolna.pl/forum/259908.html

 jakbym miała to na zajęciach to bym jakoś to
tozwiązała, niestety nie mieliśmy tego..
jakbym miała to na zajęciach to bym jakoś to
tozwiązała, niestety nie mieliśmy tego..