Trygonometria Lukas: Zapisać w postaci funkcji trygonometrycznych kąta z pierwszej ćwiartki wyrażenia:

	π
sin(−		) ?
	3

Ajtek: 430

Saizou : w tym wystarczy zapamiętać że "tylko cosinus pożera minus", zatem sin(−x)=−sin(x) tg(−x)=−tg(x) ctg(−x)=−ctg(x) ale cos(−x)=cos(x) bo to funkcja parzysta

Mila:

	π		π
sin(−		)=−sin(		) bo sin(x) jest funkcją nieparzystą.
	3		3

Lukas: Dziękuję. Jadę dalej

Mila: Szerokiej drogi!

Lukas: Mila a wytłuamczyłabyś mi nierówności trygonometryczne ?

Eta: Uważaj na zakrętach

Lukas: Eta Ty powiedziałaś, że nie ma szans.. To mam odpuścić ?

Eta: Czytaj ze zrozumieniem! napisałam : "bierz się do pracy!"

Mila: Pisz zadania będziemy Ci tłumaczyc.

Lukas:

	1
sinx>
	2

Wiem, że jest w linku ale nie bardzo rozumiem.

Mila:

	1
sinx>
	2

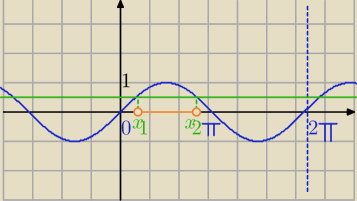
Okres zasadniczy funcji f(x)=sin(x) jest równy T=2π To co widzisz w przedziale <0,2π> powtarza się na całej osi X.

	1
Teraz rysujemy prostą y=
	2

Patrzysz dla jakich argumentów ( x−ów) wykres sinus (x) leży nad zielona prostą. Zaznaczyłam na pomarańczowo. Teraz ustalamy ile wynosi x₁ i x₂

	1		π		π		5π
sinx=		⇔x1=		, x2=π−		=
	2		6		6		6

	1		π		5π
sinx>		w przedziale <0,2π> dla x∊(		,		)
	2		6		6

Ponieważ funkcja jest okresowa to dla całej dziedziny będzie tak:

	1		π		5π
sinx>		dla x∊(		+2kπ,		+2kπ)
	2		6		6

gdy podstawisz k=1 to będziesz miał podane rozwiązanie w przedziale <2π,4π>)

Lukas: Dziękuję.

Mila: Czy coś się wyjaśniło?

Lukas: Tak, jutro jeszcze jutro wstawię jeszcze zadania do sprawdzenia, poprawy.

Lukas: cos(x)≥1

Lukas: ?

Eta: Jakie wartości przyjmuje cosinus?

Lukas: Cos [−1,1]

Eta: wniosek ........... do tej nierówności ......

Lukas: Że cos(x)=1 ?

Lukas: ?

Krystek: Tak stąd x=?

Lukas: x=0

Eta: x= k*2π , k∊C

Eta: https://matematykaszkolna.pl/strona/427.html

Lukas: Dziękuję, jutro na uczelni wolne więc można więcej zadań zrobić.