Wartość bezwzględna w wykładniku (funkcja wykładnicza) Patryk: Witam, poleceniem zadania jest "W wyniku jakich przekształceń wykresu funkcji g(x)=2^x, otrzymamy wykres funkcji f? Podaj zbiór wartości funkcji f. a) f(x)=|2^x−2| b) f(x)=2^|x| c) f(x)=2^|x+2| d) f(x)=2^|x|+2 Mam dokładne odpowiedzi w książce, ale nie rozumiem jaka jest zasada rysowania wykresu tych funkcji. Ponieważ raz najpierw rysuję się wykres funkcji y=2^x, nastepnie to co ejst pod osią x, przenosi nad oś x, po czym dopiero się przesuwa wykres, a innym razem wykres szkicuje się od razu z przesunięciem. A jeżeli bym zrobił w przykładzie w kolejności innej, niż w rozwiązaniu, to nie wychodzi to samo. A więc od czego zależy kolejność?

Kejt: https://matematykaszkolna.pl/forum/259220.html

Patryk: Własnie tam zajrzałem przed chwilą i rozumiem, że zawsze jest kolejność nast.: względem osi y > o "p" > względem osi x > o "q" Dobrze, rozumiem?

Patryk: Jeżeli tak, to kiedy trzeba odbić wykres względem danej osi?

Kacper: a) 2^x→u=[0,−2]→2^x−2→|f(x)|→|2^x−2|

Patryk: b) 2^x→f|(x)|→2^|x| c) 2^x→u=[−2,0]→2^x+2→f|(x)|→2^|x+2| d) 2^x→f|(x)|→2^|x|→u=[−2,0]→2^|x|+2 Tak? A jak z dziedziną?

5-latek: Ale Patryku pytaja o zbior wartosci a nie dziedzine

Patryk: Pomyłka A więc?

Kacper: b) f(|x|) − taki zapis c) żle (zła kolejność) d) źle (zła kolejność) W c) i d) musisz zamienić na odwrót i będzie ok

Patryk: Kacper, okej, dzięki. A jak ze zbiorem wartości? Z wykresu odczytać po prostu?

Patryk: Ponawiam pytanie. Już wiem jak doprowadzić do danej postaci funkcje i jaki jest wykres funkcji, ale nie wiem jak wyznaczyć zbiór wartości.

Kacper: Jak masz wykres, to odczytujesz

Patryk: Porobiłem wykresy i kompletnie nie pamiętam jak to się robiło z wartością bezwzględną. Każdy wykres jest nad osią x, ale 2 przykładzie 1 np rozwiązanie to <1;+∞), a ja bym wszędzie dał (0;+∞)... :c

Kacper: Ale tam są przesunięcia, które powodują zmianę zbioru wartości.

Patryk: Jakieś nakierowanie?

Patryk: To pomoże ktoś wskazać zbiór wartości? Jakiś link, cokolwiek.

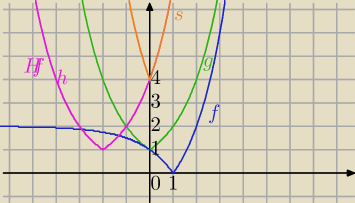
Mila: W różnych sytuacjach podchodzi się indywidualnie do problemu zbioru wartości. wykorzystujemy własności funkcji a) f(x)=|2^x−2| ≥0 Zw=<0,∞) b) y=2^x − funkcja rosnąca ( własności f.wykladniczej) 2^x>0 wykres funkcji g(x)=2^|x| powstaje przez "odbicie" symetryczne względem OY wykresu y=2^x z prawej strony OY, zatem najmniejsza wartość funkcja ma dla x=0 g(0)=2^|0|=1 Zw=<1,∞ ) c)h(x)=2^|x+2| Najpierw rysujesz y=2^x , następnie y=2^|x|, potem translacja o wektor[−2,0], nie zmienia to zbioru wartości, zatem jak poprzednio h(0)=1− najmniejsza wartość h(x) najmniejsza c) s(x)=2^|x|+2 tu rysujemy najpierw y=2^x , potem translacja o wektor [−2,0] , potem symetria względem OY. s(x) ma najmniejszą wartość dla x=0 s(0)=2²=4 − najmniejsza wartość s(x) Zw=<4,∞)

Patryk: Wielkie dzięki, kolega mi też przed chwilą wytłumaczył słownie, a tutaj mam wszystko wypisane. Dziękuję bardzo i życzę dobrej nocy!

Mila: Wzajemnie. Dobranoc