Dla jakich wartosci parametru m Hubert: Dla jakich wartosci parametru m,m∊R, rownanie m²−1=sinx/2 + sin²x/4 + sin³x/8 + sin⁴x/16 + ... ma rozwiazanie a wiec licze granice S= a₁/1−1 S= sinx/2 / 1− sinx/2 po skroceniu wychodzi ze sinx = 2m² Odpowiedz jest jakas dziwna, wiec mysle ze robie cos zle, jakies wskazowki?

Hubert: Dla jakich wartosci parametru m,m∊R, rownanie m2−1=sinx2 + sin2x4 + sin3x8 + sin4x16 + ... ma rozwiazanie a wiec licze granice S= a11−q

	sinx2
S=
	1− sinx2

po skroceniu wychodzi ze sinx = 2m²

AcidRock: Hmm... A mnie wyszło, że:

	2
sin x = 2 −
	m2

Przedstaw może obliczenia.

Mila:

	0,5 sinx		2		sinx
S=		*		=
	1−0,5sinx		2		2−sinx

	sinx
S(x)=
	2−sinx

sinx=t i t∊<−1,1>

	t		−t
S(t)=		=		przekształcamy
	−t+2		t−2

	−t+2−2		−2
S(t)=		=−1+		i t∊<−1,1>
	t−2		t−2

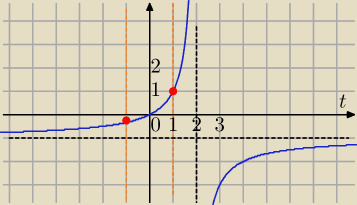
Rysujemy wykres i określamy zbiór wartości S(t) dla t∊<−1,1> funkcja rosnąca

	−2		2		1
S(−1)=		−1=		−1=−
	−1−2		3		3

	−2
S(1)=−1+		=−1+2=1
	1−2

	1
Zw=<−		,1>
	3

dla

−1
	≤m2−1≤1 istnieją rozwiązania
3

Rozwiąż nierówność

Mila: Albo bez wykresu , jak u Acid..

Mila: https://matematykaszkolna.pl/forum/258838.html