kombinatoryka zadanie: Rozmieszczenie k ponumerowanych kul w n ponumerowanych komorkach. Niech bedzie dane funkcja: f: {1, 2, 3, ..., k}→{1, 2, 3, ..., n} Liczba wszystkich roznych rozmieszczen jest rowna n^k. (k≥n; liczba kul jest wieksza badz rowna liczbie komorek) Kule pelnia role argumentow tej funkcji a komorki wartosci. f(1)=2 oznacza, ze pierwsza kula znajduje sie w drugiej komorce f(2)=3 oznacza, ze druga kula znajduje sie w trzeciej komorce (f(1), f(2), f(3), ..., f(k))−ciag k−elementowy. (2, 3, 3, 4, 1)−pierwsza kula jest w drugiej komorce, druga i trzecia kula w trzeciej, czwarta kula w czwartej, piata kula w pierwszej komorce. A czy mozna byloby napisac w tej kolejnosci: (f(3), f(1), f(2), ..., f(k)) ? Czy zawsze piszemy od f(1) potem f(2), czyli (f(1), f(2), ..., f(k))? Moglbym poprosic o sprawdzenie?

PW: Zwyczaj jest taki, że wymieniamy po kolei, według rosnących argumentów. Permutacje przyjęło się pisać jako ciąg wartości − tak jak to zrobiłeś w piątym wierszu dołu (każdy sobie policzy numer argumentu).

zadanie: Napisalem wczesniej, ze k≥n. Ale na pewno? Bo przeciez: f: {1}→{1, 2} 2¹=2 (f(1))=(1) (f(1))=(2) ale czy to jest dobrze? bo czy te ciagi nie powinny zawierac wartosci 1 i 2 jednoczesnie?

PW: Jeden ciąg f₁ = (1, 2), drugi ciąg f₂ = (2, 1)

zadanie: nie rozumiem to nie powinny byc ciagi jednoelementowe? bo mamy jeden argument ale wartosci maja byc ze zbioru {1, 2} czyli 1 i 2 musza wystapic jednoczesnie (dobrze rozumiem?) czyli ciagi (1) i (2) nie moga byc no to jak jednoelemetowe? no bo (1, 2)=(f(1), f(?) czego?)

PW: To może ja nie zrozumiałem? Serio rozważasz liczbę ciągów jednoelementowych o wartościach w zbiorze dwuelementowym? f₁ = (1) , f₂ = (2). Słowami: są dwie różne funkcje f: {1} → {1, 2} − wypisane wyżej f₁ i f₂. Nie mogą te ciągi zawierać dwu wartości jednocześnie, bo są jednoelementowe, to oczywiste − jednemu elementowi każda funkcja przyporządkowuje jeden element.

zadanie: Czyli od poczatku. Poprawna odpowiedzia sa 2 funkcje (2 ciagi jednoelementowe). (f(1))=(1) (f(1))=(2).

PW: Tak, tylko oznaczałbym je dwiema różnymi literami, np. f i g, bo tak to jest mylące.

zadanie: Czy jak mamy polecenie o wartosciach w zbiorze np {a, b} to czy te wartosci musza wystapic jednoczesnie w jednym ciagu? Pytam bo https://matematykaszkolna.pl/forum/258603.html A dokladniej: juz wiem dlaczego bo funkcja musi miec wartosci ze zbioru {a, b}. czyli np. dla zbioru {1, 2} nie moze byc (1, 1, 1) i nie moze byc (2, 2, 2)

zadanie: Co zle rozumiem?

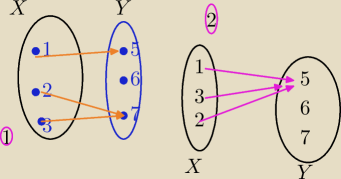
Mila: W tamtym zadaniu miałeś warunek , że funkcja ma zbiór wartości dwuelementowy. Mogło być tak jak na (1) rys. Nie mogło byc tak, jak na (2) rys. W (1) Z_w={5,7} w (2) Z_w={5}

Trivial: Zapis f : X → Y oznacza, że argumenty funkcji f są ze zbioru X, a dozwolone wartości ze zbioru Y. Możemy mieć funkcję f(x) = 1 i opisać ją przykładowo jako f : R → R f : R → N f : N → N f : N → { 1 } f : { 1 } → N ...

Mila: Niech X={x₁,x₂}, Y={0,1} Wypisz wszystkie funkcje f:X→Y i dla każdej odpowiadający ciąg. 1) f(x₁)=0, f(x₂)=0 ciąg (0,0)

Trivial: A wzór n^k działa dla dowolnych n,k ≥ 1

zadanie: 2) f(x₁)=0, f(x₂)=1 ciąg (0,1) 3) f(x₁)=1, f(x₂)=0 ciąg (1,0) 4) f(x₁)=1, f(x₂)=1 ciąg (1,1) to wszystkie bo 2²=4.

Mila: W porządku, masz dwie funkcje różnowartościowe (2) i (3). Dwie funkcje stałe (1) i (4) Dla trzech argumentów będzie jeszcze inaczej. Wypisz wszystkie funkcje dla X={x₁,x₂,x₃} i Y={0,1} f:X→Y i odpowiadające ciągi.

zadanie: Czyli zapis f : X → Y oznacza, ze X to zbior argumentow funkcji (kazdy z nich musi miec przyporzadkowana dokladnie jedna wartosc), a zbior Y to przeciwdziedzina funkcji (mozliwe jej zbiory wartosci, niekoniecznie wszystkie). W zadaniu z podanego linku byl zapis: f: 2{1, 2, 3}→{1, 2, 3, 4}. Przeciwdziedzina tej funkcji to: {1, 2, 3, 4}. Jednym z warunkow w zadaniu bylo aby ta funkcja miala dwuelementowy zbior wartosci, czyli kazdy ciag mial zawierac jednoczesnie dwa te elementy. (jakies z przeciwdziedziny) Tutaj: f: {1, 2, 3}→{1, 2} Przeciwdziedzina to: {1, 2}, ale zbior wartosci moze zawierac 1 albo 2 albo 1 i 2. ({1} lub {2} lub {1, 2}) Czyli ciag k−elementowy o przeciwdziedzinie inaczej o wartosciach w zbiorze np. {1, 2} oznacza, ze zbiorem wartosci tego ciagu (jego wyrazami) moga byc 1 albo 2 albo 1 i 2. ({1} lub {2} lub {1, 2}). Czy dobrze rozumiem?

zadanie: 1) f(x₁)=0, f(x₂)=0, f(x₃)=0 ciąg (0,0,0) 2) f(x₁)=0, f(x₂)=1, f(x₃)=0 ciąg (0,1,0) 3) f(x₁)=0, f(x₂)=0, f(x₃)=1 ciąg (0,0,1) 4) f(x₁)=1, f(x₂)=0, f(x₃)=0 ciąg (1,0,0) 5) f(x₁)=0, f(x₂)=1, f(x₃)=1 ciąg (0,1,1) 6) f(x₁)=1, f(x₂)=1, f(x₃)=0 ciąg (1,1,0) 7) f(x₁)=1, f(x₂)=0, f(x₃)=1 ciąg (1,0,1) 8) f(x₁)=1, f(x₂)=1, f(x₃)=1 ciąg (1,1,1) Wszystkie bo 2³=8.

Mila: Zgadza się. 1) Nie ma tu funkcji różnowartościowych. Teraz zastanów się kiedy można określić funkcje różnowartościowe i ile ich będzie. 2) Odnośnie 22:30 Wybrałeś jakie maja byc wartości funkcji: {1,2}, warunek− zbiór wartości dwuelementowy. Wypiszemy wszystkie funkcje 1) f(1)=1, f(2)=1,f(3)=2 ciąg (1,1,2) 2) f(1)=1, f(2)=2,f(3)=1 ciąg (1,2,1) 3) f(1)=2, f(2)=1, f(3)=1 ciąg (2,1,1) 4) f(1)=1,f(2)=2,f(3)=2 ciąg (1,2,2) 5) f(1)=2,f(2)=1,f(3)=2 ciąg (2,1,2) 6) f(1)=2, f(2)=2 ,f(3)=1 ciąg (2,2,1) ============================= 7) f(1)=1, f(2)=1,f(3)=1 funkcja nie spełnia warunków , zbiór wartości jednoelementowy 8) f(1)=2, f(2)=2, f(3)=2 funkcja nie spełnia warunków , zbiór wartości jednoelementowy

zadanie: 1) Czyli moje rozumowanie z 22:30 bylo poprawne. 2) Funkcje roznowartosciowe mozna okreslic jezeli zbior wartosci bedzie trojelementowy. Jezeli rozwazamy funkcje f: 2{1, 2, 3}→{1, 2, 3, 4}, to bedzie ich 4*3*2=24.

Mila: To trochę wyjaśnione?

zadanie: Tak, dziekuje.