Funkcje 5-latek: Witam Czy moze mi ktos wytlumaczyc takie pojecia w miare prosto i podac na kilku przykladach Nie mialem takich pojec w trakcie nauki a widze ze sie teraz pojawiaja NIe chodzi o minimum i maksimum funkcji tylko funcje minimum i maksimum

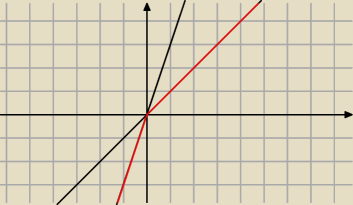
Kacper: funkcja minimum przykład: min{x,3x} co robimy? rysujemy w jednym układzie i wybieramy "kawałki" wykresu położone niżej. (wykres czerwony)

5-latek: Przepraszam ze CIe mecze mozesz podac jeszce kilka przykladow a potem to maximum

Piotr 10: Np. min (a;b) = a , gdy a < b min(;b) = b , gdy b < a

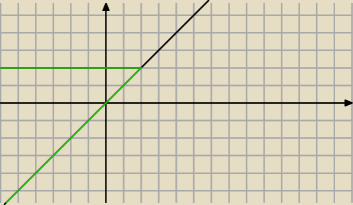
5-latek: Naszkicuje wykres funkcji min(2,x) ={2 dla x>=2 i x dla x<2 bedzie to wykres ten na zielono Ale mam jeszce takie pytanie czy zawsze w takich funkcjach mamy tak proste wzory ? jesli nie to czy moze byc np tak nim (2x+5, x−1)

Mila: f(x)=x² g(x)=4 min(4,x²)=x² dla x∊<−2,2> min(4,x²)=4 dla x<−2 lub x>2

5-latek: Dobry wieczor Milu Pozdrawiam czyli mam rozumiec ze we wzorze jakas jedna stala musi byc

5-latek: Wybaczcie proszse ale juz mi ciezko idzie zrozumienie pewnych rzeczy Dlatego zadaje tak duzo pytan

tyu: nieźle dajesz radę 5−latek

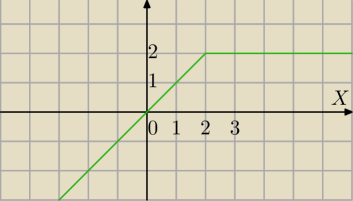
Mila: Witam serdecznie Nie, mogą być dwie funkcje. Dałam funkcję stałą, aby było łatwiejsze. Twój przykład f(x)=min(2,x) patrz rysunek 2 dla x≥2 x dla x<2

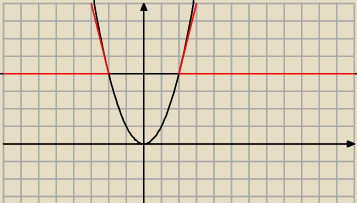
5-latek: Teraz tak max(4,x²)= 4 dla x<−2 lub x>2 max(4,x²)=x² dla xnalezy (−oo −2> U<2,oo) czy dobrze ?

5-latek: Juz widze ze zle bedzie mak(4,x²=4 dla <−2.2>

5-latek: dziekuje rowniez za poprawienie tamtego rysunku Juz co lapie Najwazniejszse to dobrze zrozumiec

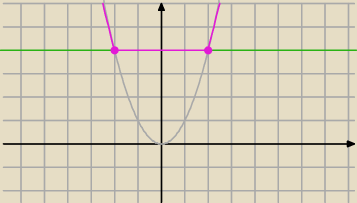
Mila: f(x)=max(4,x²) f(x)=x² dla x≥2 lub x≤2 f(x)=4 dla x∊(−2,2)

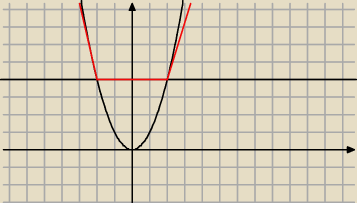
5-latek: Poprawiam rysunek z godz 22:00

Mila: Zgadza się .

5-latek: Czyli jeszce trzeba pocwiczyc . Twoja pomoc Milu bezcenna

5-latek: Nie wiem czy moze byc takie tlumaczenie Ja sobie tlumacze to tak po tych przykladach minimun −−−−− to conajmniej maximum −−−−−to conajwyzej

Mila: Ja tak − to co leży niżej to minimum.

5-latek: Dobry wieczor Milu pozdrawiam serdecznie. Myslalem ze juz wiem A tu jednak zonk chodzi o ten przyklad . https://matematykaszkolna.pl/forum/258545.html Nie rozumiem go jednak bo skoro 1 minum to myslalem ze bedzie xnalezy <1 +oo) czyli do calego zbioru R brakuje przedzialu (−oo,1)\0 Okazuje sie ze to jest bledna myslenie Co zle pomyslaem w tym przykladzie ? J sugerowal rozpatrzyc przedzial (0,1) ale przyznam sie nie wiem dlaczego

Kacper: Najpierw patrzysz na dziedzinę, a potem wybierasz kawałki "które są niżej"

5-latek: Czesc Kacper na razie troche trudno mi to zrozumiec

5-latek: Musze dokladnie popatrzec na ten wzor ktory napisal wczoraj Piotr10

Kacper: bierzesz wykresa i paczysz idziemy po wartościach ujemnych dla x. Niżej jest hiperbola, czyli

	1		1
dla x<0 min(1,		)=
	x		x

Teraz dodatnia część. Ponieważ w "1" obie funkcje się przecinają, to będziemy mówić o 2 przedziałach:

	1
dla 0<x<1 min(1,		)=1
	x

	1		1
dla x>1 min(1,		)=
	x		x

	1
dla x=1 minimum jest 1 oraz
	x

5-latek: Ja sie paczę a tu Paczków Teraz zrozumialem . Naprawde Dzieki bardzo