f(x)=min(1,1/x) whatever:

	1
Czy dany punkt należy do wykresu funkcji? f(x)=min(1,		)
	x

A(0,1) Prosze o pomoc

J: Nie ... bo punkt A(0,1) nie należy do dziedziny funkcji...

5-latek:

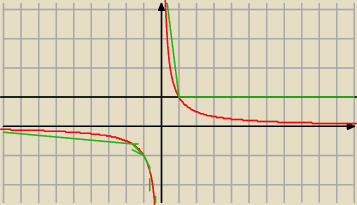
	1
min(1,		)=1 dla∊ <1,oo)
	x

	1		1
min(1,		=		dla x ∊(−oo,1)\{0}
	x		x

Czy dobrze zaznaczylem ten wykres fej funkcji na zielono ?

J: Cześć .. ... nie bardzo ...zauważ: f(1) = min(1,1) = 1

	1		1
f(2) = min(1,		) =
	2		2

	1		1
f(3) = min(1,		) =
	3		3

....

	1
f(x) =		... dla x ∊ (1,+∞)
	x

5-latek: Witam J Dziekuje . A myslalem ze juz zrozumialem . Jednak jeszce trzeba pare przykladow rozwiazac

J: ..... spróbuj przeanalizować przedział: (0,1) ..

5-latek: Tak zrobie . Tylko jak wroce z warsztatu , bo o 11 jade dalej czyscic samochod do konserwacji

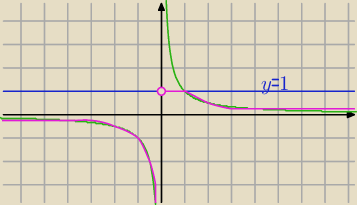
Mila: D=R\{0} x=0

	1
f(x)=min(1,		)
	x

daras: [F[Mila] ] powiedz mi jaki jest sens zapisywania w ten sposób funkcji? przecież można zapisać to jako nierówność w dwu przedziałach

Mila: No cóż, różne są teraz zadania, które mają jakiś cel bliżej mi nieznany.Może to chodzi o skrócony zapis. Macierz odwrotna w arytmetyce mod(13) też mnie śmieszy. Pewnie dlatego, że nie znam zastosowania.

5-latek: Przepraszam ze tak dlugo nie odpisywalem ale analizowalem ten rysunek

5-latek:

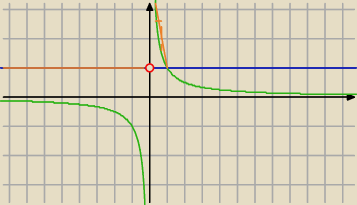
	1
Milu a wykres max(1,		) wedlug mnie bedzie wygladal tak
	x

bo 0 nie nalezy do dziedziny

Mila:

	1
f(x)=max(1,		)
	x

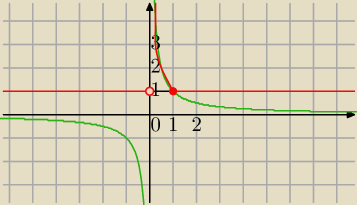
Zapomniałeś o jednym fragmencie.

5-latek: Tak Milu zapomnialem dziekuje CI bardzo . wroce do tego jak bede przerabial wlasnosci funkcji to wtedy poproszse Cie o jakie przyklady Jeszce raz wielkie dzieki

Mila: