Geo. analityczna
Matematyka z nazwy : Oblicz obwód trójkąta , którego jednym z wierzchołków jest punkt przecięcia prostych.
y=x+1 i y=2x−2 a pozostałe wierzchołki są punktami przecięcia tych prostych z osią OX.
21 wrz 21:07
5-latek:
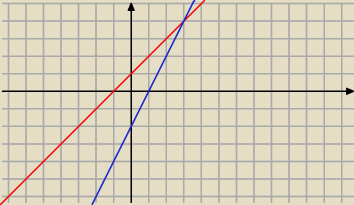
Tak wyglada rysunek do tego zadania
21 wrz 21:09
Matematyka z nazwy : No tak z tego rysunku wiem , że
A(1,0)
B(−2,0)
21 wrz 21:11
Matematyka z nazwy : |AB|=3
21 wrz 21:14
5-latek: B(−1,0)
A punkt przeciecia prostych jakie ma wspolrzedne ?
21 wrz 21:14
Matematyka z nazwy : Nie mam pomysłu jak obliczyć to przecięcie czy to wynika z f.
?C(1,2) ?
21 wrz 21:15
5-latek: Popraw |AB|=2
A punkt przeciecia mozesz przeciez odczytac z rysunku C(3,4)
lub wyliczy algebraicznie
Przyrownujesz obie funkcje do siebie
x+1=2x−2 wylicz x i potem wyliczone x podstaw np do y=x+1 i wylicz y
Wiec moze to policz tutaj
21 wrz 21:21
Matematyka z nazwy : −x=−3
x=3
y=4
C(3,4)
|AC|= √32
21 wrz 21:26
Matematyka z nazwy : |BC|= √41
21 wrz 21:27
Matematyka z nazwy : Miałem racje |AB| = 3
21 wrz 21:27
Matematyka z nazwy : ale AC i BC są źle
21 wrz 21:29
5-latek: Punkt C dobrze i tera zobacz na ten rysunek czy jest tak samo
|AB| widze z rysunku ze =2
Pozostalych tzn AC i BC nie licze wiec przestaw obliczenia sam/a
A(1,0) C(3,4)
AC= √(3−1)2+(4−0)2= √4+16=√20= √4*√5=2√5 wiec masz zle
Oblicz teraz dlugosc odcinka BC
21 wrz 21:33
Matematyka z nazwy : W odp. wynik są następujące 3+3√2 + 3√5
21 wrz 21:34
21 wrz 21:35
5-latek: Nie patrz na odpowiedz bo moze byc zla
21 wrz 21:36
Matematyka z nazwy : No nie wiem zapytam się najwyżej jutro pani
21 wrz 21:38
5-latek: A po co sie pytac jutro
Masz juz wyliczony punkt przeciecia Tak ? jest to punkt C(3,4)
Teraz masz taka funkcje y=x+1 Masz obliczyc miejsce zerowe tej funkcji tzn wyliczyc taki x
dla ktorego wartosc tej funkcji =0 to postawiamy do wzoru 0=x+1 to −x=1−0 to −x=1 to
x=−1 (zgadza sie z rysunkiem −czerwona linia ) czyli miejce zerowe tej funkcji to B(−1,0)
TEraz liczymy miejsce zerowe funkcji y=2x−2 to 0=2x−2to −2x=−2−0 to −2x=−2 to x=1
(patrz wykres niebieski ) czyli miejsce zerowe tej funkcji to A(1,0)
Ale skoro chcesz to pytaj Pani −−tylko podaj jej te funkcje a nie inne
21 wrz 21:47
Mila:
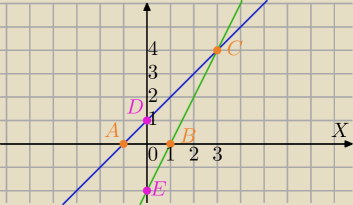
k: y=x+1
miejsce zerowe:
x+1=0
x=−1
A=(−1,0)
m: y=2x−2
2x−2=0
x=1
B(1,0)
C:
Punkt przecięcia prostych
2x−2=x+1
x−2=1
x=3
y=3+1=4
C=(3,4)
|AB|=2
|BC|
2=2
2+4
2⇔|BC|
2=20
|BC|=
√4*5
|BC|=2
√5
|AC|=
√42+42
|AC|=
√16*2
|AC|=4
√2
OBw
ΔABC=2+4
√2+2
√5
Rozważmy ΔCDE: przecięcie prostych z osią OY
|DE|=3
|DC|=
√32+32=3
√2
|CE|=
√33+62=
√9+36=
√45=
√9*5=3
√5
Ob
ΔCDE=3+3
√2+3
√5
Teraz sprawdź jaka jest treść zadania.
21 wrz 22:25
Matematyka z nazwy : Mila dzięki

21 wrz 22:32
 Tak wyglada rysunek do tego zadania
Tak wyglada rysunek do tego zadania
 k: y=x+1
miejsce zerowe:
x+1=0
x=−1
A=(−1,0)
m: y=2x−2
2x−2=0
x=1
B(1,0)
C:
Punkt przecięcia prostych
2x−2=x+1
x−2=1
x=3
y=3+1=4
C=(3,4)
|AB|=2
|BC|2=22+42⇔|BC|2=20
|BC|=√4*5
|BC|=2√5
|AC|=√42+42
|AC|=√16*2
|AC|=4√2
OBwΔABC=2+4√2+2√5
Rozważmy ΔCDE: przecięcie prostych z osią OY
|DE|=3
|DC|=√32+32=3√2
|CE|=√33+62=√9+36=√45=√9*5=3√5
ObΔCDE=3+3√2+3√5
Teraz sprawdź jaka jest treść zadania.
k: y=x+1
miejsce zerowe:
x+1=0
x=−1
A=(−1,0)
m: y=2x−2
2x−2=0
x=1
B(1,0)
C:
Punkt przecięcia prostych
2x−2=x+1
x−2=1
x=3
y=3+1=4
C=(3,4)
|AB|=2
|BC|2=22+42⇔|BC|2=20
|BC|=√4*5
|BC|=2√5
|AC|=√42+42
|AC|=√16*2
|AC|=4√2
OBwΔABC=2+4√2+2√5
Rozważmy ΔCDE: przecięcie prostych z osią OY
|DE|=3
|DC|=√32+32=3√2
|CE|=√33+62=√9+36=√45=√9*5=3√5
ObΔCDE=3+3√2+3√5
Teraz sprawdź jaka jest treść zadania.
