Wyznacz ekstrema lokalne funkcji. Daniel: Wyznacz ekstrema lokalne funckji f(x) = 3x⁴ − 8x³ + 6x² − 1. Obliczyłem pierwszą pochodną, która wynosi f'(x) = 12x³ − 24x² +12x (po uproszczeniu wynosi) f'(x)= x³−2x²+x. Przyrównałem pierwszą pochodną do zera: x³−2x²+3=0. Problem polega na tym, że nie mam pojęcia co teraz należy zrobić. Czy mógłby ktoś krok po kroku wyjaśnić dalszą część zadania?

PW: Nie, panie kolego f '(x) = 12(x³ − 2x² + x) Takie "uproszczenia" kosztują. A przyrównując do zera zamienił pan x na 3 nie wiadomo dlaczego.

Tadeusz: ... NIE MA TAKIEGO UPROSZCZENIA ! f'(x) = 12x³ − 24x² +12x f'(x)= 12(x³−2x³+x) lub f'(x)=12x(x²−2x+1) lub f'(x)=12x(x−1)² dalej chyba jasne

Daniel: Dzieki za wyprowadzenie z błedu, no, ale właśnie nie wiem co teraz mam f'(x)=12x(x²−2x+1) i co należy teraz zrobić?

Mila: Szukać kandydatów na ekstrema wśród miejsc zerowych pochodnej,⇔ trzeba rozwiązać równanie (najlepiej z ostatniej wersji Pana Tadeusza) 12x*(x−1)²=0

PW: Przyrównać pochodną do zera: f '(x) = 0 ⇔ 12x(x−1)² = 0 ⇔ x=0 ∨ x= 1. Jeżeli funkcja f ma ekstrema lokalne, to tylko w punktach 0 lub 1. Czy rzeczywiście są tam ekstrema − poznajemy po dalszym punkcie "przepisu na badanie funkcji".

5-latek: https://matematykaszkolna.pl/strona/387.html Popatrz tam na zadanka Daniel

Daniel: Czyli moge to robić tak: 12x(x−1)²=0, że 12x(x−1)(x+1) wtedy miejsca zerowe będą wynosiły x=1 i x= (−1)? Próbowałem też obliczyć delte z (x²−2x+1), ale delta wyszła mi −2. Gdy mam miejsca zerowe, jaki jest dalszy krok? Musze je wstawić do pierwotnego wzoru funkcji i obliczyć?

Daniel: Czyli dla miejsc zerowych 1 i −1 liczę f(1)= (wstawiam 1 zamiast x) dla f(−1) wstawiam −1 zamiast x i wynik to będa moje ekstrema i to wszystko tak?

5-latek: Jak z tego x²−2x+1 mogla wyjsc CI delta −2 ? przeciez z tego Δ=0 Przeciez to jest wzor skroconego mnozenia x²−2x+1=(x−1)² .

Mila: Ja jestem dość leniwa i nie liczę następnej pochodnej, wystarczy zbadanie w któym punkcie pochodna zmienia znak. Tu widać, że tylko w x=0 z ujemnego na dodatni po przejściu przez 0, zatem to będzie minimum. f(0)=−1 w x=1 punkt przegięcia.

5-latek: Dobry wieczor Milu Pozdrawiam

PW: Nieeee, zerowanie się pochodnej to tylko warunek konieczny istnienia ekstremum: jeżeli istnieje ekstremum w x₀, to f '(x₀) = 0. Wcale nie znaczy to, że twierdzenie odwrotne jest prawdziwe, z tego że f '(x₀) = 0 wcale nie wynika, że w x₀ funkcja f ma ekstremum. Typowy nieśmiertelny przykład f(x) = x³. f '(0) = 0, ale w x₀=0 nie ma ekstremum! Przeczytaj hasło "warunek dostateczny istnienia ekstremum funkcji różniczkowalnej".

PW: O, zanim wstukałem swoje marudzenia, to Mila już wyjaśniła

Daniel: Czyli w miejscu gdzie pochodna zmienia swój znak tam znajduje się ekstremum tak? Gdybym narysował sobie wykres tej funkcji, tam gdzie pochodna zmienia znak tam jest ekstremum?

Daniel: Jedno pytanie tylko, obliczyłem miejsce zerowe, które wynosi x0=1, jest tylko jedno miejsce zerowe tak? co musze zrobić z tym miejscem zerowym?

Daniel: teoretycznie wiem, jak dojść do poprawnego wyniku i zadanie gotowe, ale nie rozumiem skąd to się bierze. Doszliśmy do momentu gdzie x0=1. Dlaczego widać, że funkcja zmienia znak tylko w x=0 z ujemnego na dodatni po przejściu przez 0?

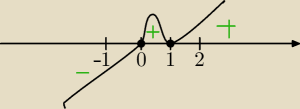
Mila: Tak. Możesz też badać drugą pochodną, tak Ci chyba będzie łatwiej, bo widzę, że słabo Ci to wychodzi. Źle rozwiązałeś równanie. 12x*(x−1)²=0⇔ 12x=0 lub (x−1)²=0⇔ x=0 lub x−1=0 x=0 lub x=1 pierwiastek podwójny f'(x)<0 dla x<0 ⇔f(x) jest malejąca dla x∊(−∞,0) f'(0)=0 f'(x)>0 dla x∊(0,1) ⇔f(x) rosnąca dla x∊<01) ⇔ f(0)=−1 minimum f(x) f'(1)=0 tu zbadaj czy jest punkt przegięcia

PW: bo w przepisie na f ' jest czynnik (x−1)² − zarówno dla x < 1 jak i dla x > 1 jest to wyrażenie dodatnie, więc znak f '(x) nie zmienia się "przy przejściu przez 1".

Daniel: Dobra mam to, dzieki wielkie za pomoc, po prostu źle znajdowałem miejsca zerowe. Dzięki jeszcze raz!

Mila: