wyznacz wszystkie wartości parametru m dla których równanie |(x+3)^2 - 1| = |m+2 Kreska: wyznacz wszystkie wartości parametru m dla których równanie |(x+3)² − 1| = |m+2| ma dwa rozwiązania różnych znaków

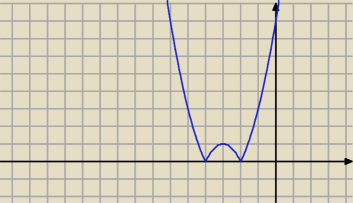
Godzio: Rysujemy parabolę f(x) = (x + 3)² − 1, a następnie to co jest na dole odbijamy na górę. Odczytujemy z wykresu dla jakich prostych mamy dwa punkty przecięcia i argumenty odpowiadające tym punktom są różnych znaków, widać, że dla y > 8 mamy to o co nas pytają, stąd: |m + 2| > 8 ⇔ m ∊ (−∞,−10) U (6,∞)

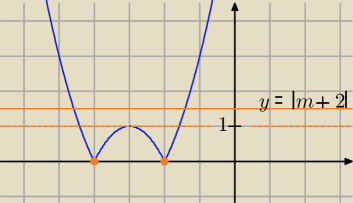
Bogdan: Ilustracja do zadania. Dwa rozwiązania dla |m + 2| = 0 lub dla |m + 2| > 1

pigor: ..., z własności modułu liczby: |(x+3)²−1| = |m+2| ⇔ (x+3)²−1= m+2 v (x+3)²−1= −m−2 ⇔ ⇔ f(x)=(x+3)²= m+3 v f(x)=(x+3)²= −m−1 i f(0)= 9, to warunki zadania będą spełnione ⇔ m+3>9 v −m−1>9 ⇔ ⇔ m>6 v m<−10 ⇔ m∊(−∞;−10) U (6;+∞) . ...

Eta: @ Lukasa https://matematykaszkolna.pl/forum/257598.html teraz zastosuj to do zadania z "białą flagą"

Lukas: Już myślę nad rozwiązaniem