prostokąt trojkat obliczanie
gustawa:
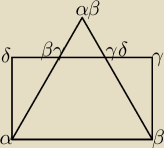
Prostokat αβγδ i trójkąt rownoboczny αβαβ sa położone tak jak na rysunku. Bok αβ prostokąta ma
długość 30cm a bok βγ 15cm. Bok γδ prostokata przecina boki α αβ i β αβ trójkąta w punktach βγ
i γδ. Jakie jest pole czworokata αβγδγβ
7 wrz 21:52
Janek191:
Te literki mi się nie podobają

7 wrz 22:44
gustawa: Literki sa takie bo nie umiałam wstawić normalnych

7 wrz 22:52
Janek191:
Każdy punkt musi być oznaczony inną literką .
Literki masz na klawiaturze

7 wrz 23:02
Janek191:
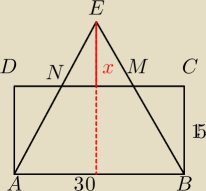
7 wrz 23:08
gustawa: Janek co dalej prosze pomóż
7 wrz 23:09
Eta:
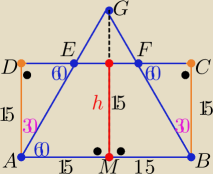
7 wrz 23:17
gustawa: I nadal nie rozumiem
7 wrz 23:20
Janek191:
Mamy
oraz
| | √3 | |
h = x + 15 = 30* |
| = 15 √3 ⇒ x = 15√3 − 15 = 15*( √3 − 1) |
| | 2 | |
więc
| 15*(√3 − 1) | | 15√3 | |
| = |
| |
| I MN I | | 30 | |
| √3 − 1 | | √3 | | 30*( √3 − 1) | |
| = |
| ⇒ I MN I = |
| = 10√3*( √3 − 1) |
| I MN I | | 30 | | √3 | |
I MN I = 30 − 10
√3
I M C I = 15 − 0,5 I MN I = 15 − ( 15 − 5
√3) = 5
√3
Pole czworokąta ABMN
P = 30*15 − 15* I MC I = 450 + 15* 5
√3 = 450 + 75
√3
=============================================
7 wrz 23:26
Janek191:
Pomyłka − miało być
P = 450 − 75√3
==============
7 wrz 23:27
Eta:
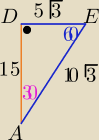
|DE|=|FC|=5
√3 to |EF|=30−10
√3 i
h=15
| | 30+30−10√3 | |
O(trapezuABEF)= |
| *h= (30−5√3)*15= 5*15(6−√3)= 75(6−√3) |
| | 2 | |
7 wrz 23:28
7 wrz 23:29
Janek191:
Lub
P = 0,5 *( 30 + I MN I )*15 = 0,5*( 30 + 30 − 10√3 )*15 = (30 − 5√3)*15 = 450 − 75√3
7 wrz 23:30
Janek191:
Lub
P = 0,5 *( 30 + I MN I )*15 = 0,5*( 30 + 30 − 10√3 )*15 = (30 − 5√3)*15 = 450 − 75√3
7 wrz 23:31
Eta: 
7 wrz 23:33
ruda: Pomóżcie mi z tym 2 bo ja już zwariowalam nic nie rozumiem prosze bardzo
7 wrz 23:33
 Prostokat αβγδ i trójkąt rownoboczny αβαβ sa położone tak jak na rysunku. Bok αβ prostokąta ma
długość 30cm a bok βγ 15cm. Bok γδ prostokata przecina boki α αβ i β αβ trójkąta w punktach βγ
i γδ. Jakie jest pole czworokata αβγδγβ
Prostokat αβγδ i trójkąt rownoboczny αβαβ sa położone tak jak na rysunku. Bok αβ prostokąta ma
długość 30cm a bok βγ 15cm. Bok γδ prostokata przecina boki α αβ i β αβ trójkąta w punktach βγ
i γδ. Jakie jest pole czworokata αβγδγβ





 |DE|=|FC|=5√3 to |EF|=30−10√3 i h=15
|DE|=|FC|=5√3 to |EF|=30−10√3 i h=15
