Trygonometria:) Blue: Zbiorem wartości funkcji f(x) = sin⁴x +cos⁴x jest zbiór: A.<0,1>

	1
B. <		,1>
	2

C. <0,2>

	1
D. <0,		>
	2

Doszłam tylko do czegoś takiego: sin⁴x +cos⁴x = (sin²x+cos²x)² −2sin²xcos²x = −2sin²xcos²x+1.. Jak to dalej przekształcić

bezendu: https://matematykaszkolna.pl/forum/251988.html

ICSP:

	1
−2sin2xcos2x = −		(sin2x)2
	2

daras: no widzisz Blue wystarczy wpisac w tutejszą wyszukiwarkę A ZAOSZCZĘDZISZ MNÓSTWO CZASU SOBIE I INNYM

Blue: Bezendu, ale to zadanie, które dałeś jest zupełnie inne niż to, które dodałam... ICSP dziękuję

Blue: ICSP, a nie ma może jeszcze prostszego jakiegoś sposobu na wyznaczenie tego zbioru wartości?

bezendu: Na podstawie tego mogłaś w analogiczny sposób określić zbiór wartości, jak byś spojrzała dokładnie a, nie tylko przeleciała wzrokiem to byś wiedziała o tym...

Mila: 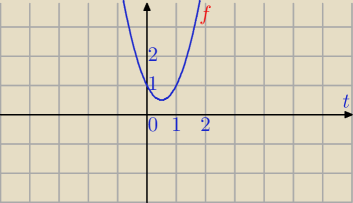Blue, sposób ICSP jest prosty i elegancki. Musisz znać dobrze wzory i tożsamości trygonometryczne.Zajmij się tym w najbliższym wolnym czasie. Podam Ci inny sposób, ale nie wiem, czy prostszy? Chyba nie. f(x)=sin⁴x +cos⁴x f(x)=sin⁴x+(1−sin²x)²⇔ f(x)=2sin⁴x−2sin²x+1 Podstawienie : sin²x=t, t∊<0,1> f(t)=2t²−2t+1

	1		1
tw=		∊<0,1) dla t=		f(t) ma wartość najmniejszą
	2		2

	1		1		1		1
f(		)=1*		−2*		+1=		wartość najmniejsza
	2		4		2		2

f(0)=1 i f(1)=1 1 − wartość największa f(t) dla t∊<0,1>

	1
Zw=<		,1>
	2

=============

PW: Jeżeli spojrzeć na to zadanie pod kątem "jak szybko rozwiązać zadanie testowe w teście jednokrotnego wyboru", to odpowiedź jest natychmiastowa. Należy wyeliminować wszystkie odpowiedzi, w których najmniejszą wartością funkcji jest 0. sin⁴x + cos⁴x = 0 byłoby możliwe tylko wtedy, gdyby oba składniki były jednocześnie zerami; tak nie jest, wystarczy spojrzeć na wykresy. Pozostaje odpowiedź B, bo jedna jest prawdziwa. To raczej spryt a nie matematyka, ale tego najwyraźniej oczekuje CKE dając 35 zadań na 170 minut.

Kacper: Testowe mają to do siebie, że nie trzeba rozwiązywać zadań

PW: Dlatego sądzę, że nie zdołałbym zdać matury na 100%, zawsze kusi żeby sprawdzić. A ile minut zajęłoby uczniowi rozwiązanie sposobem Mili? Ja też łapię się na takie rozumowania i złoszczę się: czego oni oczekują od tych biednych uczniów?

Kacper: Że nie zdadzą Małe sprostowanie − to zadanie z poziomu rozszerzonego (oni mają 180 minut i około 20 zadań) Właśnie mam w ręku informator, w którym nie pisze ile tych zadań będzie Może ktoś ma takie info?

Mila: Tak w zadaniach testowych często należy wyrozumować odpowiedź. Tu wyjątkowo prosto, w innych trzeba cos policzyć.

Blue: Mila, interesujące rozwiązanie... Kacper, chyba ok.18 zadań, ale może to się różnić o jakieś dwa zadania

Blue: albo np. w tych zadaniach testowych jak ktoś nie zna tożsamości dokładnie [czytaj Blue], to może sobie popodstawiać i zobaczyć co pasuje

Mila: Wszelkie chwyty dozwolone.Oby prowadziły do celu.