Parametr Halka: Proszę o pomoc w zadaniu Dla jakich wartości parametru a równanie ma rozwiązania: sin²x+cosx+a²=0

Godzio: sin²x = 1 − cos²x oraz wstawmy t = cosx Otrzymujemy równanie kwadratowe: − t² + t + 1 + a² = 0 Równanie takie ma rozwiązanie gdy Δ = 0 i t₀ ∊ <−1,1> lub Δ > 0 i jeden z pierwiastków albo oba należą do przedziału <−1,1>

Halka: No tak, w takim wypadku delta wyszła mi 5+4a². Odpowiedź −1≤a≤1. Dlatego nie mam pomysłu co dalej zrobić.

razor: −cos²x+cosx+1 = −a² cos²x−cosx−1 = a² niech cosx = t, t∊<−1,1> Liczę współrzędne wierzchołka tej funkcji

	1
tw =		− należy do przedziału
	2

	1		1		1		5
f(		) =		−		− 1 = −
	2		4		2		4

f(−1) = 1+1−1 = 1 f(1) = 1−1−1 = −1

	5
ZW = <−		, 1>
	4

	5
a2 ∊ <−		, 1>
	4

rozwiąż dalej

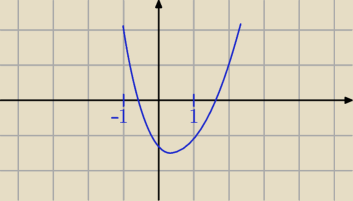Godzio: Przekształcę sobie równanie: t² − t − 1 − a² = 0 (bo już rysunek zrobiłem, nie chciało mi się poprawiać ) Warunki: Δ > 0 −− to wiemy 1^o f(1) < 0 f(−1) > 0 2^o f(1) > 0 f(−1) < 0 Łącząc 1^o i 2^o możemy napisać prościej: f(1) * f(−1) < 0 Narysuj sobie inną sytuację i zrób podobnie (chodzi o dwa pierwiastki należące do <−1,1>)

Godzio: razor pokazał szybszy sposób (mój zatem pozostawiam do analizy − takie rozumowanie przydaje się w funkcji kwadratowej z parametrem)