 cześć wszystkim
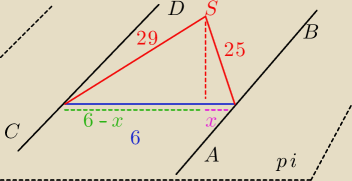
Dwie proste równoległe AB i CD odległe od siebie o 6 cm leżą na płaszczyźnie. Punkt S leży poza
tą płaszczyzną w odległości 25 cm od prostej AB i 29 cm od prostej CD. Wyznacz odległość
punktu S od płaszczyzny.
proszę o wytłumaczenie dlaczego Mila w podpowiedzi z 2 lut 2012 16:04 zamieszczonej tutaj
jako trzeci post https://matematykaszkolna.pl/forum/125198.html napisała, by zastosować m.in.
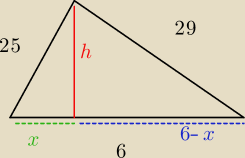
takie równanie (6+x)2 +h2 =292 Podobne równanie ułożył pigor, więc ono jest
dobre.
Ale dlaczego nie można tutaj zastosować minusa, tak jak zrobiła to Basiek (6−x)2 i
ja na rysunku
cześć wszystkim
Dwie proste równoległe AB i CD odległe od siebie o 6 cm leżą na płaszczyźnie. Punkt S leży poza
tą płaszczyzną w odległości 25 cm od prostej AB i 29 cm od prostej CD. Wyznacz odległość
punktu S od płaszczyzny.
proszę o wytłumaczenie dlaczego Mila w podpowiedzi z 2 lut 2012 16:04 zamieszczonej tutaj
jako trzeci post https://matematykaszkolna.pl/forum/125198.html napisała, by zastosować m.in.
takie równanie (6+x)2 +h2 =292 Podobne równanie ułożył pigor, więc ono jest
dobre.
Ale dlaczego nie można tutaj zastosować minusa, tak jak zrobiła to Basiek (6−x)2 i
ja na rysunku  Cały odcinek to c=6. Jego część to x, więc druga część to 6−x
Cały odcinek to c=6. Jego część to x, więc druga część to 6−x

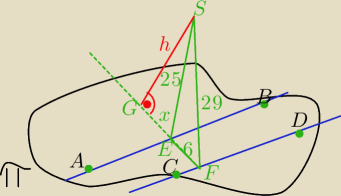 ΔSEF− Δprostokątny
292=62+252−2*6*25 cos (∡E)⇔
841=36+625−300*cos (∡E)
180=−300*cos (∡E)
ΔSEF− Δprostokątny
292=62+252−2*6*25 cos (∡E)⇔
841=36+625−300*cos (∡E)
180=−300*cos (∡E)
| 18 | ||
cos (∡E)=− | <0⇔ΔSEF− Δrozwartokątny | |
| 30 |
