Geometria przestrzenna.
Basiek :
Geometria przestrzenna.
Zad.
1. Dwie proste równoległe AB i CD odległe od siebie o 6 cm leżą na płaszczyźnie. Punkt S leży
poza tą płaszczyzną w odległości 25 cm od prostej AB i 29 cm od prostej CD. Wyznacz odległość
punktu S od płaszczyzny.
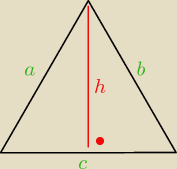
Dochodzę do momentu, gdzie mam obliczyć to h...
i dane
a=29
b=25
c=6
(część odcinka c nazwałam x, druga to będzie 6−x)
Z: x,h>0 i x<6
więc z Pitagorasa
h=
√292−x2
h=
√252−(6−x)2
po porównaniu x=21 <− sprzeczne. Dlaczego nie wychodzi, skoro całość wydaje się dobra?
2 lut 15:46
Basiek : Noo proszę no, jakby nie patrzeć poległam przy tw. Pitagorasa.
2 lut 15:51
Mila: Basiek, to jest trudne. Napisałam Ci wskazówkę, ale gdzieś zniknęła. Obliczyłam kąt i wyszło mi
, że tam jest kąt rozwarty (cos <0)
Zrób rysunek przestrzenny ( ja bazuję na ostrosłupie) i wyjdzie, jeśli założysz :
(6+x) 2 +h 2 =292
i h2 +x2 = 252
2 lut 16:04
Basiek : Okej, rozumiem, dzięki
Mila 
Z czego obliczałaś cos
2 lut 16:06
pigor: a ja tak to ...
widzę,
d
2=25
2−x
2=29
2−(x+6)
2 ⇒ (x+6)
2−x
2=29
2−25
2 ⇔ 6(2x+6)=4*54 ⇔ x+3=18 ⇒
x=15 , zatem np. d
2=25
2−15
2= 10* 40 = 400 ⇒
d=20 − szukana
odległość . ...
2 lut 16:11
Basiek : Hm, to sprowadza się do tego samego, tak mi się wydaje
Pigor Tylko zapis przysparza mi
bólu głowy.
Ale dziękuję.
Okej, pytania powyżej nie było. Wyliczyłam sobie z tw. cosinusów, nawet mi wyszło, że α≈143 st.
Hm, no i konstruktywny wniosek wyciągnięty z zad. : czasem opłaca się sprawdzać cos. kątów. Kto
by to pomyślał...
2 lut 16:14
Mila: Pigor inaczej widzi, a ja muszę mieć rysunek i tak zinterpretowałam.Też mi nie wychodziło i
dlatego badałam kąty.
2 lut 16:18
Basiek : Gut, rozumiem
jeszcze raz dziękuję
Póki co zmykam, potem będę się pewnie męczyła z dalszymi zad.
Pa.
2 lut 16:20
Basiek : Trochę nie na temat, ale mam pytanie: Jak wyznaczyć prostą BC, gdy:
B=(−3,−2),C=(−3,4) , wiem , że z postaci kierunkowej nic nie będzie...., ale ogólna powinna
wyjść jakoś... z tym, że mnie same sprzeczności wychodzą LUB za mało danych.
Proszę o pomoc, bo nie będę mogła spać...
2 lut 18:48
AC:
Równanie prostej to
x=−3
2 lut 18:51
Basiek : Boże... Normalnie ... brak mi słów.
Dziękuję. Jestem idiotką
2 lut 18:52
AC:
Każdy może mieć chwilę słabości
2 lut 18:55
Basiek : Byle nie za długo...
Jeszcze jedno pytanie: a gdyby punkty miały wspólną współrzędną rzędnych?
np. A(−3,−1) B(2,−1)
2 lut 18:56
AC:
to:
y=−1
2 lut 19:02
Basiek : Ekhem...
Nie skomentuję.
W każdym razie bardzo dziękuję
2 lut 19:03
pigor: ...
y = −1 − funkcja stała − wykres to prosta II do osi Ox ., przecież wiesz .
2 lut 19:03
Basiek : No wiem, tylko rozmyślałam nad przykładem pierwszym i hm, w mojej głowie zrobiła się mała
rewolucja układu współrzędnych. Chyba nie wyjdzie mi to na dobre...
2 lut 19:06
krystek: gdyby przełożyc na geomerie w pierwszy przykładzie a=tgα a w tym przypadku prosta jest
prostopadła do osi OX i nie istnieje tg90 stopni! Stad nie mogłas wyliczyć a
2 lut 19:12
Basiek : No właśnie,doszłam do tych samych wniosków.
| | y1−y2 | |
Próbowałam potem wyliczyć a ze wzoru |
| , gdzie mianownik wyszedł mi równy |
| | x1−x2 | |
0... Poczułam się więc hm, zagubiona, więc przybiegłam do Was
2 lut 19:16
Eta:
1/ to sprawdzasz, to czy x
A= x
B ⇒ AB: x= x
A
czy y
A= y
B ⇒ AB: y= y
A
| | yB−yA | |
i dopiero wtedy gdy xA≠xB i yA≠yB lecisz wzorem aAB= |
| −xA} |
| | xB | |
2 lut 19:33
Eta:
Ciut mi wylazł x
A
2 lut 19:34
Basiek : No dobra... , ale jeśli nawet yb−ya =0, to a istnieje, tylko jest równy 0, więc prosta jest
prostą równoległą do OX.
... ? oO
2 lut 19:35
krystek: OK.
2 lut 19:37
Basiek : Okej. Dobra, dziękuję. Dowiedziałam się chyba więcej niż chciałam. Jeszcze raz stokrotne
dzięki!
2 lut 19:41
krystek: @Eta, a ten wczorajszy przypadek "wypociny" odezwał się po korepetycjach?
2 lut 19:43
Eta:
krystek i ........ ja
.......... "jak stare dobre wino "
2 lut 19:44
Eta:
Ależ skąd
..... może nie był na tych korkach !( a nam nie wierzy
2 lut 19:46
krystek: Wyjatkowo trudny przypadek !
2 lut 19:52
2 lut 22:02