Geo :D
Blue: W trójkącie ostrokątnym ABC boki AC i BC mają odpowiednio długości 15 i 14. Oblicz długości
odcinków, na jakie ortocentrum trójkąta dzieli wysokość AK, jeśli wysokość ta ma długość 12
Wiem już teraz jakie trójkąty są podobne, ale mogę wyliczyć tylko pole i drugą wysokość i co
dalej
Podstawy ani trzeciej wysokości nie wyliczę, bo niby jak
20 sie 18:56
Blue: Pomoże ktoś?
20 sie 19:45
20 sie 19:52
pigor: .., niech
|CK|=y , to
|KB|=14−y dla uproszczenia zapisu,
O − ortocentrum (punkt przecięcia się wysokości ΔABC, a
|OK|=x=? , to
|OA|=12−x=?, to z ΔAKC i tw. Pitagorasa oraz
podobieństwa ΔCOK∼ΔAKB mamy np. taki układ równań :
y2=15
2−12
2= 3*27=
81 i
xy = 14−y12 ⇒ y=9
i
x9 =
14−912 ⇒ 4x=15 ⇔ x=
|CK|=3,75 i 12−x=
|KA|=8,25. ...
20 sie 20:02
Janek191:
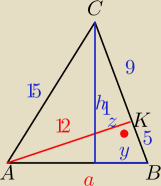
Mamy x
2 + 12
2 = 15
2
x
2 = 225 − 144 = 81
x = 9
14 − 9 = 5
a
2 = 12
2 + 5
2 = 144 + 25 = 169
a =
√169 = 13
P = 0,5 *14*12 = 84
P = 0,5 a*h
1 = 0,5*13*h
1 = 6,5 h
1
6,5 h
1 = 84
y
2 = 14
2 − h
12 = ...
12 − z = ....
20 sie 20:17
Blue: Dzięki
20 sie 20:59