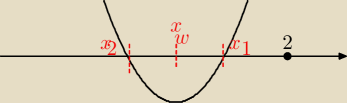
f.kwadratowa tyu: wyznacz te wartości parametru m, dla których każde z rozwiązań równania mx²−(m²−3m+2)x+2m−6= jest mniejsze od 2. I − gdy m=0, −2x−6=0 ⇒ x=−3, czyli dla m=0 wartość x jest mniejsza niż 2 II − gdy m≠0 1/ Δ≥0 2/ a>0 3/ f(2)>0 4/ x_w<2 ad1/ Δ=(m²−3m+2)² i Δ≥0 więc (m²−3m+2)²≥0 ⇒ m∊R, bo kwadrat czegokolwiek jest zawsze większy lub równy zero ad2/ m>0 ⇒ m∊(0;+∞) ad3/ 4m−2(m²−3m+2)+2m−6>0 4m−2m²+6m−4+2m−6>0 −2m²+12m−10>0 /:(−2) m²−6m+1<0 Δ_m=16=4² m₁=1 m₂=5 m∊(1;5) ad4/

m2−3m+2
	< 2 na 99% to źle rozwiązuję
2m

dla m≥0 nie zmieniam znaku nierówności

m2−3m+2
	< 2 / *2m
2m

m²−3m+2 < 4m m²−7m+2 < 0 Δ_m=41 √Δ_m=√41

	7−√41		7+√41
m1=		m2=
	2		2

	7−√41		7+√41
m∊(		;		)
	2		2

dla m<0 m²−7m+2 > 0

	7−√41		7+√41
więc m∊(−∞;		) U (		; +∞ )
	2		2

prawidłowy wynik to (−∞;0> U (1;5), który mi z tych obliczeń nie wychodzi. Czy ktoś mógłby wskazać mi gdzie robię błąd

Piotr 10: A czemu ramiona paraboli ni mogą być skierowane w dół ?

J: Źle liczysz Δ ... Δ = [− (m² − 3m + 2)]² − 4*m*(2m − 6)

J: No i to co napisał Piotr 10 ... ramiona mogą być też w dół.

tyu: mogą, ale to wtedy warunki trzeba dostosować (a>0 i f(2)<0), a wynik jest ten sam , więc przyjąłem, że są skierowane w górę.

Piotr 10: https://matematykaszkolna.pl/forum/220418.html podobne zadanie rozwiązywałeś

tyu: no właśnie je rozwiązałem, ale tutaj jakiś błąd mi wychodzi. Nie wiem gdzie on jest.

J: Źle masz policzoną Δ.

Piotr 10: m*f(2) > 0 i to załatwia ramiona paraboli

tyu: Δ − błąd. Prawidłowa to (m²−3m−2)²

tyu: przeliczę jeszcze raz. Dzięki za pomoc.

Kacper: " wynik jest ten sam , więc przyjąłem, że są skierowane w górę." nie możesz sobie niczego przyjmować Jeśli mogą być dwa przypadki to oba należy rozważyć.

tyu: to trzeba liczyć dwa przypadki − gdy ramiona są w górę albo w dół błędna Δ: (m²−3m+2)²≥0 więc m∊R, prawidłowa Δ: (m²−3m−2)²≥0 więc m∊R, tutaj chyba ten błąd nie zaważył na przedziale, do którego należy m

Kacper: Albo skorzystać z uwagi Piotrka z godziny 13:13 To, że przypadkiem dostałeś ten sam wynik nie oznacza, że za błędy nie byłbyś ukarany

tyu: właśnie, bo widziałem podobny warunek w innym zadaniu czyli m*f(2) > 0 obliczę w ten sposób, że liczę sobie *f(2) > 0 i to co zostanie po lewej stronie mnożę przez m zapis m*f(2) > 0 oznacza 1/ m>0 i f(2) > 0 albo 2/ f(2) <0 i m<0

tyu: teraz właśnie robię podobne zadanie. Wyznacz te wartości parametru m, dla których jeden z pierwiastków równania mx² −(2m+1)x + m−2=0 jest ujemny, a drugi większy od 5. i tam takie warunki 1/ Δ>0 2/ x₁*x₂<0 3/ m*f(5)<0 ad 1/ Δ=12m+1

	− 1
m>
	12

ad 2/

m − m
	<0 i m≠0
m

przypadek, gdy m >0 to nie zmieniam znaku m−2<0 m<2 przypadek, gdy m <0 to zmieniam znak m−2>/0 − sprzeczność ad 3/ m*f(5)<0 m[25m−5(2m+1) + m− 2] <0 m[16m−7]<0

	7
m∊(0;		)
	16