f.kwadratowa
tyu:
czy ktoś mógłby mi wyjaśnić warunek nr 2 i 3 w tym zadaniu.
Wyznacz wszystkie wartości parametru m, dla których każde z dwóch różnych rozwiązań równania
x
2+x+m=0 jest większy od m.
1/ Δ>0
2/ f(m)>0

3/ x
w>m − z tego wynika, że wierzchołek ma być na prawo od m, tylko chyba m to linia
pionowa

10 sie 22:00
Eta:
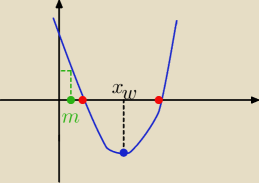
10 sie 22:09
10 sie 22:10
PW: Gdyby f(m) < 0, oznaczałoby to że m leży między rozwiązaniami (między rozwiązaniami są takie x,
dla których f(x) < 0). Warunek 2) gwarantuje zatem, że oba rozwiązania są albo z prawej strony
m, albo z lewej. Warto to narysować.
Dodanie warunku xw > m daje pewność, że co najmniej jedno rozwiązanie leży po prawej stronie
m.
Dlatego 2) i 3) razem wzięte dają pewność, że oba rozwiązania leżą po prawej stronie m.
10 sie 22:13
tyu: dziękuję. To jest podobny przykład, ale tam jest liczba rzeczywista, którą łatwiej sobie
umieścić na osi, a nie niewiadoma "m".
10 sie 22:15
tyu: wiem, że dobry wynik dadzą takie warunki
Δ>0
| −b − √Δ | |
| > m czyli mniejszy pierwiastek jest bliżej +∞ niż "m". |
| 2a | |
Ale znając życie, zapomnę że takie 2 proste warunki można ułożyć, więc staram się zrozumieć te
3 z pierwszego postu.
10 sie 22:21
tyu: czyli tutaj m traktuję jako x. Jeśli f(x)<0 i ramiona paraboli idą do góry, to wtedy pkt m leży
między rozwiązaniami.
10 sie 22:37
 3/ xw>m − z tego wynika, że wierzchołek ma być na prawo od m, tylko chyba m to linia
pionowa
3/ xw>m − z tego wynika, że wierzchołek ma być na prawo od m, tylko chyba m to linia
pionowa 
