trygonometria tyu: sinx*sin2x = cosx*cos2x są tutaj https://matematykaszkolna.pl/forum/57030.html dwa rozwiązania tego zadania Jedno napisał Godzio (post − 17 wrz 2010 00:36) drugie sowa (post − 17 wrz 00:41)

	π		2kπ
Wynik z książki to x=		+
	6		3

rozwiązanie przedstawione przez sowę kończy się na

	1		−1
cosx=0 v sinx=		v sinx=
	2		2

jeśli policzy się to dalej to

	π
(dla cosx=0) x=		+ kπ lub
	2

	1		π		5π
(dla sinx=		) x=		+ 2kπ lub x=		+ 2kπ lub
	2		6		6

	−1		7π		11π
(dla sinx=		) x=		+ 2kπ lub x=		+ 2kπ
	2		6		6

rozwiązanie, które zaprezentował Godzio, ma wynik

	π		kπ
x=		+
	6		3

a w książce jest inaczej. Wie ktoś gdzie jest błąd Nie rozumiem też tego przekształcenia w rozwiązaniu, które zaprezentował Godzio, −(cosx*cos2x − sinx*sin2x) = 0 cos(x + 2x) = 0

Saizou : Godzio pisząc −(cosx*cos2x−sinx*sin2x) chciał zastosować wzór cos(α+β)=cosα*cosβ−sinαsinβ odpowiednio dla kątów α=x i β=2x

Saizou : to jest rozwiązanie sowy zapisane w postaci jednego wzorku

	2		1
α=		π=		π
	6		3

	π		1
x=		+		kπ
	6		3

tyu: Dziękuję za zainteresowanie. Ale jak dla sowy z trzech wyników wyszedł jeden ?

tyu: no i dla sowy wyszedł inny wynik niż w książce. Chyba że w książce jest błąd...

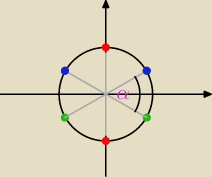
Saizou : widzisz to kółko, które narysowałem oznaczyłem tam kąty wraz z okresowości (niekiedy okresowość się pokrywa z pierwotnym punktem (gdy T=2π))

	π		π
i tak czerwona kropka x=		+kπ, zaznaczam kąt		i dodaję okresowość (dlatego dwie
	2		2

czerwone kropki) i analogicznie z pozostałymi kątami

	π
zauważasz że między punktami jest taki sam kąt α=
	3

tyu: aha. Czyli tak to ma być. Dziękuję.