równanie Lukas: Rozwiąż równanie x²+3x−18+4√x²+3x−6=0 4√x²+3x−6=−x²−3x+18=0 /² x⁴+6x³−43x²−156x+420=0

	−3−√33		−3+√33
D=(−∞,		>suma<		,∞)
	2		2

(x−2)(x+5)(x²+3 x−42)=0 x=2∊D x=−5∊D

	−3−√177
x=		∊D
	2

	−3+√177
x=		∊D
	2

?

Godzio: Pomyśl jeszcze nad dziedziną i założeniu dzięki, któremu możesz podnosić do kwadratu

Godzio: Naczy o dziedzinie nie, o założeniu

Lukas: x²+3x−6≥0 Δ=33 √Δ=√33

	−3−√33
x1=
	2

	−3+√33
x2=
	2

co źle jest ?

Godzio: Bardziej mi chodzi, że −x² − 3x + 18 musi być nieujemne, żeby w ogóle podnosić do kwadratu.

Saizou : kurcze, nie miałem klinkąc wysłać, przperaszam

Godzio: http://paczaizm.pl/content/wp-content/uploads/no-co-zrobisz-nic-nie-zrobisz.jpg

Saizou : i ten wąs

Godzio: Jak widać, 2 rozwiązania u Lukasa nie spełniają równania

Lukas: kolejny raz mówię, że nic chcę gotowców... To mam nie ustalać dziedziny ?

pigor: hmm..., równanie to ma sens ⇔ (*) x²+3x−6 ≥0 , a wtedy x²+3x−18+4√x²+3x−6= 0 ⇔ √x²+3x−6²+4√x²+3x−6−12= 0 ⇔ ⇔ √x²+3x−6=−6 v √x²+3x−6=2 ⇔ x∊∅ v x²+3x−6= 4 ⇔ x²+3x−10=0, stąd i z (*) ⇔ (x= −5 i 25−15−6= −1<0) v (x=2 i 4+6−6=4 ≥0) ⇒ x∊{2} . ...

Godzio: Ustaliłeś dziedzinę − JEST OK Teraz masz równanie √.... = .... i chcesz podnieść do kwadratu, ale żeby to uczynić, musisz być PEWNY, że obie strony są nieujemne. Dlaczego? Bo lewa jest ≥ 0, no to prawa również musi być nieujemna, inaczej sprzeczność, zgoda?

Godzio: Zasypany gotowcami

Lukas: ok czyli przenoszę na drugą stronę i też rozwiązuje nierówność tak ? a potem część wspólna tych nierówności czy co ?

Lukas: Nawet nie patrzę na tę gotowce i robię inaczej bez żadnych zmiennych !

Godzio: −x²−3x+18 ≥ 0 z tego bierzesz drugi zbiór, i w rozwiązaniu sprawdzasz część wspólną tego zbioru i dziedziny, której ustaliłeś wcześniej

Lukas: Dziękuję

pigor: ..., radzę ci jednak najpierw uczyć się na gotowcach, lub przykładach , bo to co piszesz powyżej to wierutne bzdety ; no to powiedziałem co widziałem − dostanie mi się i niech tam ... bo nic tu po mnie

Lukas: Uczę się tak jak mi wygodnie i nie mam zamiaru uczyć się na gotowcach ''Wierutne bzdety''−uczę się więc mam prawo się mylić a Ty sam jak się uczyłeś też robiłeś błędy i chyba zapomniał wół jak cielęciem był ?

Godzio: Sobota wieczór, pora się relaksować, a nie denerwować, cześć !

Eta: Oj,Lukas, Lukas Musisz nauczyć się pokory, bo inaczej to nikt nie będzie chciał Ci pomagać, Co do "cielątka", to zapamiętaj : "pokorne cielę dwie matki ssie" ! Przeproś przy najbliższej okazji pigora ,bo najwyraźniej Go obraziłeś! Nie będę się więcej rozpisywała na ten temat( komentarze zostaw dla siebie, nawet i teraz) Zabieraj się za rozwiązanie tego zadania np; tak: 1 sposób − dziedzina − przenieś wyrazy bez pierwiastka na prawo − określ kiedy prawa strona jest nieujemna ( i wyznacz dla niej część wspólną z dziedziną) − teraz dopiero możesz podnieść równanie obustronnie do kwadratu − i podaj odp ........ 2 sposób − zastosuj podstawienie : √ x²+3x−6=t, t≥0 − to: x²+3t−6=t² i x²+3t−18= t²−12 i działaj.......... −po wyznaczeniu "x" sprawdź z dziedziną − i podaj odp.................. Ja wolę sposób 2/ Powodzenia i bądź grzeczny

Lukas: Dziękuję i tylko takiego schematu mogę się uczyć na pamięć !

Saizou : Etuś były rozwiązania ale ktoś je usunął xd a rozwiązałem 2 sposobem xd

Saizou : Lukas w matematyce nie uczy się na pamięć tylko intuicyjnie (bardzo pomaga) do każdego zadanka trzeba podchodzić inaczej, a nuż będzie łatwiej xd

Kacper: spać dzieciaki

Lukas: o tej porze ?

Eta: Na Ciebie też już jakaś "Baltazar..ka" pewnie czeka

Metis: A mnie ciekawi jak wygadałoby rozwiązywanie tego równanka bez podnoszenia do kwadratu

Saizou : jakaś Bogini pewnie bo Kacper ofiarował kadzidło, czyli symbol boskości

Eta: Widzę,że pigor "walnął się" 25−15−6=4>0 To równanie ma dwa rozwiązania : x= −5 v x= 2 Co można sprawdzić.....

Eta: @Metis ..... czytasz uważnie posty? 2 sposób

Saizou : z ciekawości, kto usunął moje rozwiązanie ?

Eta: Ja , ..... może Mila

Saizou : może, no cóż i tak było to omyłkowo wysłane wiec może i dobrze xd

Eta: Saizou ........ zadanie z czworokątem wciąż czeka

Saizou : dzisiaj inna pasja, a mianowicie rysowanie, wybacz Eto

Metis: Juz widzę Eta ale szczerze mówiąc pierwszy raz sie spotykam z takim zapisem Muszę go sobie przyswoić bo z tego co widzę to przydatny

Eta:

Eta: Saizou .... czworokąt też trzeba narysować

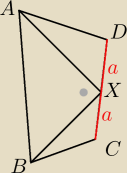
Saizou : coś takiego chyba tam było i wykazać że AD + BC ≥ AB

Eta: Dokładnie tak

Saizou : jał o dziwo zapamiętałem xd

Eta: Brzydkie słowo........ (

Saizou : jał, o dziwo, czy zapamiętałem, czy xd (jeśli to słowo)?

Eta: No jak tam Lukasio? masz już rozwiązanie tego równanka?

Lukas: przecież już rozwiązałem 19:33

Saizou : ale odpowiedzi nie wymierne są złe xd

Eta: Ajj sorry ... nie widziałam

Saizou : * niewymierne, kiepsko z moim polskim to tej godzinie

Metis: Saizou masz juz dowód do tego czworokąta ?

Saizou : Jak chcesz możesz to rozwiązać, bo było kierowane do wszystkich xd

Metis: Ciekawe to zadanko Chce znać odpowiedź A zadanko zostawiam ekspertom

Metis: Ale myslałem nad nierównościami trójkątów

Saizou : nierówność da ci ograniczenie nieostre, wiec musi być "coś" jeszcze xd

Lukas: Teraz jeszcze muszę poćwiczyć tę podstawienia i temat mam za sobą.

Metis: "coś" Parę osób których znam przeprowadziłoby dowód za pomocą linijki

bezendu: I Ty pewnie wśród nich ?

Eta: Saizou teza jest taka: |AD|+|BC|>|AB|

Saizou : https://matematykaszkolna.pl/forum/255484.html Zobacz post z 30 lip 2014 22:33

Eta: Sorry .......pomyliłam się

Eta: Nierówność ma być ostra

Eta: @Lukas Z tego tematu zostały jeszcze nierówności z pierwiastkami .

Metis: Nie bezendu , ja nie Ja preferuję ekierkę

Kacper: To ja wrzucę jedną prościutką √x+3>x−2

Piotr 10: √x+3 = t ⋀ t ≥ 0

Kacper: Ja wolę zwykłą analizę

Kacper: Czekamy na Lukasa żeby rozwiązał

ae: Na razie każdego strofuje

Lukas: x+3≥0 x≥−3 D=<−3,∞) x−2≥0 x≥2 x∊<2,∞) √x+3>x−2 /² x+3>x²−4x+4 x²−5x+1>0 √Δ=√21 x₁=U{5−√21}[2}

	5+√21
x2=
	2

Kacper: Brak komentarza, to jest nierówność nie równanie. Prawdę mówiąc tylko za dziedzinę masz w sumie dobrze Jeszcze raz i napisz co robisz i dlaczego, egzaminator nie będzie się domyślał za ciebie

Lukas: 1.Dziedzina 2. przenoszę na drugą stronę to co nie jest pod pierwiastkiem 3.sprawdzam kiedy prawa storna jest ≥0 4.rozwiązuję nierówność

Saizou : pomyśl nad momentem podnoszenia do kwadratu xd √x+3>x−2 i dajesz założenie x−2≥0, a co gdy x−2<0

Iv: Co do pierwszego zadania, to można sprawdzić: x²+3x−18+4√x²+3x−6=(√x²+3x−6+2)²−16=[√x²+3x−6+2+4][√x²+3x−6+2−4]

Eta:

Kacper: Lukas odpowiedz na pytanie Saizou

Lukas: To nierówność sprzeczna ?

Kacper: dla x=0 √3>−2 nierówność sprzeczna?

Eta: Lukas...pomyśl jeszcze raz

Lukas: Myślę i nic.

Saizou : pomyśl ! x−2<0 i x+3≥0 (bo dziedzina)⇒x∊<−3:2) gdy weżniemy liczbę z tego przedziału to nierówność √x+3> x−2 będzie spełniona dla każdego x ∊<−3:2)

Lukas: Myślę cały czas.. Ale coś chyba nie mam dnia.

WueR: √x+3≥0 dla x∊R −3 ≤ x < 2 ⇔ −5 ≤ x − 2 < 0

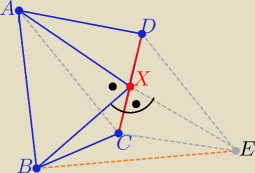
Eta: No i nikt nie rozwiązał zadania W czworokącie wypukłym ABCD punkt X jest środkiem boku CD i miara |∡AXB|=90^o Wykaż ,że : |AD|+|BC|>|AB| wykreślamy równoległobok ACED z własności równoległoboku CE|=|AD| ΔABX i ΔBEX są przystające z cechy (bkb) zatem: |BE|=|AB| Z nierówności trójkąta BCE ⇒|CE|+|BC|> |BE| ⇔ |AD|+|BC|>|AB| c.n.w

Eta:

Metis: Saizou za długo zwlekałeś

Saizou : ale to było zadanko od Ety i nie tylko dla mnie

Metis: Wiem wiem

Eta: