P#1
Lukas:
Dobry wieczór. Trochę mnie nie było więc wracamy ostro do nauki !
1. Rozwiąż równanie
√x−1+√x+2
Proszę tylko o wskazówki
28 lip 22:11
Ajtek: Dziedzina
.
I pokaż całe równanie, nie tylko część.
28 lip 22:12
Saizou :
dziedzina i pamiętaj że do kwadratu możesz podnosić tylko jedy lewa i prawa strona są tego
samego znaku xd
28 lip 22:13
rybka:
Wskazówka: gdzie tu jest znak równości?
28 lip 22:13
Lukas:
√x+1+√x+2=3
28 lip 22:15
Mila:
Do kwadratu i sprawdzić otrzymane rozwiązanie.
28 lip 22:16
Saizou :
ale najpierw dziedzina xd
x+2≥0 i x+1≥0
potem do kwadratu i pomyśl dalej xd
28 lip 22:17
ZKS:
Metoda analizy starożytnych jak podpowiada Mila.
28 lip 22:18
Lukas:
Mogę sobie tak podnosić do kwadratu ?
x+1+√x+2=9
x+√x+2=8 ?
28 lip 22:20
Ajtek: Cześć
saizou, ZKS .
28 lip 22:20
Saizou :
| | 17−√41 | |
pozdrawiam przy sprawdzaniu pierwiastka x= |
| |
| | 2 | |
28 lip 22:21
Saizou :
możesz, dlaczego? po lewa i prawa są nieujemne
√x+2=8−x (kiedy możesz podnieść do kwadratu + zrób założenie )
28 lip 22:22
rybka:
Taki sposób
podstawienie :√x+2=t, t≥0 ⇒ x+2=t2 ⇒ x+1=t2−1
28 lip 22:22
Saizou :
Cześć Ajtek kopę lat cię nie widziałem xd
28 lip 22:23
ZKS:
Siemka
Ajtek.
Dziedzinę dla osoby mało wprawionej będzie ciężko ustalić.
28 lip 22:23
Lukas:
rybka to teraz mam:
x+2=t2
Czemu takie podstawienie ?
28 lip 22:24
rybka:
√t2−1+t=3 /2
.......
28 lip 22:25
Lukas:
hmm
?
28 lip 22:26
Saizou :
co ja za x policzyłem
tak to jest jak się liczy równanie
√x+1+√x+2=3
28 lip 22:28
rybka:
28 lip 22:32
Saizou :
Etuś jak tam nad morzem ?
28 lip 22:33
Ajtek: Ale już jestem i nie zamierzam nigdzie się gubić
28 lip 22:33
rybka:
Pływałam w ciepłej wodzie
jak to "rybka"
28 lip 22:34
Ajtek: Mogłem się domyślić
rybko , łap na przynętę
28 lip 22:34
Saizou :
Ajtek zwiedzałeś Amazonię jak jechałeś do Warszawy
28 lip 22:36
rybka:
Aj
tE k
28 lip 22:36
Ajtek: Powiedzmy
saizou .
Co Wy z tym AjtEk
, najpierw
pigor teraz
Eta?
28 lip 22:38
Saizou : nie śmiećmy już Lukasowi bo nas prześwięci xd
28 lip 22:39
rybka:
Widzisz w Ajtek
Eta ?
28 lip 22:40
Lukas:
Ja się zastanawiam nad tym co napisała Mila
28 lip 22:40
rybka:
Lukas zaraz się wkurzy
28 lip 22:40
Lukas:
Wkurzam się jak ktoś pisze mi rozwiązanie od A do Z nie dając pomyśleć albo robi zdania karząc
podać tylko wynik
28 lip 22:44
Saizou :
Mila proponuje rozwiązanie bez dziedziny, czyli metodę analizy starożytnych, chodzi o to
że
liczysz pierwiastki równanie nie zwracając uwagi na dziedzinę i wychodzą ci "jakieś tam" x, a
natępnie wstawiasz je do wyjściowego równania i sprawdzasz, które liczby są OK
28 lip 22:44
Ajtek: Po prostu zastanawiam się dlaczego tak piszecie mojego nika?
28 lip 22:44
rybka:
Aj
tE k ⇒
AtE =
EtA
28 lip 22:46
Ajtek: Aaaaaaaha
28 lip 22:47
rybka: 
28 lip 22:48
Lukas:
Dwa nie koniecznie musisz jak już wyżej ktoś napisał zastanawiać się nad tym nickiem...
W końcu to forum matematyczne..
podnoszę do kwadratu
x−1+√x+2=9
x+√x+2=10
t2=√x2
x+t2=10
i co dalej ?
28 lip 22:50
Saizou :
mam pytanie to jest funkcja elementarna po przejściach
f(x)=
√x h(x)=x+2
(f ◯ g)=
√x+2=p(x)
x−1+
√x+2=k(x)
(f ◯ k)=
√x−1+√x+2
dobrze rozumiem
28 lip 22:50
Saizou :
x+
√x+2=10
√x+2=10−x i dać założenie że 10−x≥0, żeby móc podnieść do kwadratu
28 lip 22:51
Lukas:
Mila to założenie mam dać przed podniesieniem do kwadratu ?
28 lip 22:52
rybka:
@Lukas
To w końcu, jakie jest pierwotne równanie:
√x+1√x+2=3 ? czy √x−1√x+2=3 ?
zobacz co podałeś : 22: 15
28 lip 22:54
Lukas:
√x−1+√x+2=3 !
28 lip 22:58
Saizou :
ja proponuję najpierw założyć tylko że
x+2≥0 (bo to pod pierwiastkiem) i
x−1≥0 (bo suma liczb nieujemnych jest nieujemna, te liczby to x−1 i √x+2 )
28 lip 23:01
Mila:
Zmieniłeś równanie,
Podnosisz obustronnie do kwadratu i dostajesz to co u Saizou 22:51 , teraz 10−x≥0 i do
kwadratu.
rozwiązujesz równanie i sprawdzasz rozwiązania.
28 lip 23:06
Saizou :
a ktoś sprawdzi moją funkcję po przejściach
28 lip 23:07
Mila:
Albo tak jak pisze Saizou, od początku z założeniami.
28 lip 23:08
rybka:
Metoda starożytnych:
po podniesieniu do kwadratu:
√x+2=10−x
prawa strona musi być nieujemna : 10−x≥0 ⇒ x.....
i podnieś jeszcze raz obustronnie do kwadratu
jako odp: podaj x≤10
i sprawdź równanie pierwotne..........
A teraz idę na herbatkę
28 lip 23:14
Ajtek: Z prundem?
28 lip 23:18
tomker: Drodzy forumowicze, biję się z pewnym tematem od kilku godzin, a mianowicie:
Szukam wzoru na obliczanie odległości od punktu (x,y) do odcinka o współrzędnych (x1, y1) i
(x2, y2). Generalnie chodzi o znalezienie najkrótszej drogi od tego punktu do tego konkretnego
odcinka (nie prostej).
Wspomożecie mnie poradą?
28 lip 23:19
Saizou : ale bryza teraz wieje z lądu do morza (chyba) wiec uważaj, zeby cię tam nie wywiało
28 lip 23:19
28 lip 23:20
Saizou : a odcinek zawiera się w prostej
28 lip 23:21
tomker: Widziałem tę stronę, ale mi chodzi o odcinek
28 lip 23:21
Ajtek: tomker, a co wiesz o tym odcinku, poza jego współrzędnymi?
28 lip 23:21
tomker: chce znaleźć najkrótszą drogę do tego odcinka
28 lip 23:22
tomker: nic
28 lip 23:22
Ajtek: saizuo już rozwiązał problem.
28 lip 23:23
Saizou :
tomker załóż nowy post
28 lip 23:24
Saizou :
Ajtekk nie zupełnie xd
28 lip 23:24
Ajtek: saizou, jak nie jak tak
. Napisane jest odcinek, a odcinek zawiera się w prostej. Jeśli
nie jest to odcinek tylko krzywa, to nic o niej nie wiedząc, nie znajdziemy odległości.
28 lip 23:26
tomker: ten wzór wylicza prostopadłą do prostej
mam założyć nowy post?
28 lip 23:26
Saizou :
najlepiej
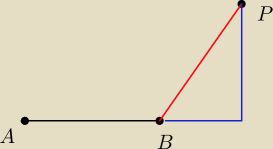
Ajtek ale szukamy najkrótszej drogi, popatrz np. na sytuację
najkrótsza droga do odcinka AB to czerwona krecha a nie niebieska
28 lip 23:28
28 lip 23:28
Ajtek: A faktycznie, tego nie wziąłem pod uwagę
.
28 lip 23:30
Saizou : załóż nowy post xd
tamten wzór opisuje tylko sytuację gdy najkrótszą drogą jest odcinek prostopadły do AB
28 lip 23:31
tomker: ok
28 lip 23:32
tomker: dzięki wam
28 lip 23:32
5-latek: Czesc
Ajtek
Zapytam Cie tak jak w tej piosence .
Gdzie zes ty bywal czarny baranie ?
Tylko nie odpowiadaj mi ze
We mlynie we mlynie itd
28 lip 23:34
Saizou :
5−latek witaj, a to nie była kołysanka
28 lip 23:34
Ajtek: Cześć
5−latek .
Już wiesz gdzie byłem
28 lip 23:35
5-latek: Czesc Saizou
Oczywiscie ze nie .
Przeciez nie bede mu spiewal tak jak Pani K. Pronko. [N[ Niech moje serce kolyszse Ciebie do
snu]]
28 lip 23:38
5-latek: Przeczytalem ze sie zagubiles (cokolwiek to znaczy)
Ale dobrze ze juz jestes z nami
28 lip 23:43
Ajtek: Przestępca zawsze wraca na miejsce zbrodni
28 lip 23:45
5-latek: OK
28 lip 23:49
Lukas:
Mila Dziękuję Ci za wskazówki rybka Tobie również. Ale nie rozumiem użytkownika Ajtka który
robi tylko spam, niszcząc przydatne wątki.. Mnie osobiście przeszkadza spamowanie nie wnoszące
nic do tematu i przeszkadza w nauce, konwersacji z osobami które chcą mi pomóc.
29 lip 14:54
Mila:
Dokończyłeś?
29 lip 15:41
Kacper: Czy w tym temacie pojawiło się rozwiązanie jakiegoś zadania?
29 lip 16:41
Mila:
Niestety nie.
29 lip 17:11
Lukas:
Nie dokończyłem. Chcę zrobić to zadanie na dwa sposoby. Najpierw 22:16 a potem tak jak podała
Eta
29 lip 17:55
Mila:
Napisz. Sprawdzę.
29 lip 17:57
Lukas:
√x−1+√x+2=3
1, x−1+√x+2=9
2. x+√x+2=10 co mam zrobić w drugim kroku ?
29 lip 17:59
Mila:
√x+2=10−x teraz zał. 10−x≥0 bo lewa jest nieujemna, natepnie obustronnie do kwadratu.
29 lip 18:01
Lukas:
Lewa strona jest nieujemna ? Przecież x może wynosić powyżej 10 wtedy będzie ujemna ?
29 lip 18:11
Mila:
L=√x+2 ≥0 to prawa też ma być nieujemna.
29 lip 18:14
Lukas:
Zawsze to zachodzi ?
29 lip 18:22
Mila:
tak
√25=5
√0=0
wynik pierwiastka kwadratowego z liczby nieujemnej jest ≥0
29 lip 18:29
Lukas:
Dobrze czyli założenie 10−x≥0
x+2=100−20x+x2
x2−21x+98=0
Δ=49
√Δ=7
x1=7 x2=14
29 lip 18:37
Eta:
Podaj właściwą odp, bo x≤10
29 lip 18:38
Lukas:
x=7
Dziękuję teraz sposobem rybki chcę zrobić
29 lip 18:39
Eta:
29 lip 18:40
Mila:
Dobrze.
29 lip 18:40
Lukas:
√x−1+
√x+2}=3 /
2
x−1+
√x+2=9
√x+2=10−x
t=x+2 może tak być czy musi być t
2=x+2 a może być t=
√x+2
29 lip 18:47
Eta:
podstawiasz : t=√x+2 i t≥0
t2=x+2
29 lip 18:50
Lukas:
ale to t jest po podniesieniu już do kwadratu
t2=100−20x+x2 ?
29 lip 18:55
Eta:
Moim sposobem, tak:
√x−1+√x+2=3 teraz podstawiaj ........... ( jak napisałam 18:50
29 lip 18:55
Eta:
Nie możesz mieć dwu zmiennych ! tylko jedną "t"
29 lip 18:56
Lukas:
x+2=100−20x+x2
x2−21x+98=0
x=7 i x=14
29 lip 18:59
Eta:
Pomieszałeś 1 sposób z 2 sposobem
2 sposób
√x+2=t, t≥0 ⇒ x+2=t2 ⇒ x−1=t2−3
√t2−3+t=3 /2 , t≥0
...............
x=...........
29 lip 19:05
Eta:
W tym co napisałeś 18:57 brakuje założenia x≤10
29 lip 19:07
Lukas: Ok, już poprawiłem.
29 lip 19:13
Eta:
Jedziemy dalej
Rozwiąż równania:
zad1/
√22−x−
√10−x=2
zad2/
√x2−2x+1=5−2x
29 lip 19:26
Eta:
zad3/
√x−3+
√2x+1=2
√x
zad4/
√2−x+
√x−1=
√x−5
Idę teraz na dobry kisiel
29 lip 19:30
Lukas:
1.
√22−x−√10−x=2
Nie wiem jak to zrobić ? Wskazówka ?
29 lip 20:16
MQ: Przenieść np. √10−x na drugą stronę i podnieść stronami do kwadratu.
29 lip 20:21
Lukas: też tak myślałem ale i tak dostanę cały czas pieerwiastek
√22−x=2+√10−x /2
22−x=10−x+4√10−x+4
8=4√10−x /4
2=√10−x
10−x≥0
10−x=4
x=6
29 lip 20:27
Eta:
1/ określ dziedzinę
podaj odp:
29 lip 20:31
Lukas:
x∊(−∞,10>
x=6 ?
29 lip 20:33
Eta:
zad1/ 2sposób ( choć w tym przypadku 1 sposób łatwiejszy)
√10−x=t, t≥0 ⇒ 10−x=t2 ⇒ 22−x=t2+12
√t2+12 −t=2 ⇒ √t2+12=t+2 |2 t= ........ 10−x=t2 ⇒ x=......
29 lip 20:36
Lukas: dobrze zrobiłem ?
29 lip 20:37
Eta:
Sprawdź i sam odpowiedz czy dobrze ? bo kogo zapytasz na maturze?
29 lip 20:44
Lukas:
Ok, a dziedzina poprawnie ?
29 lip 20:48
Eta: tak
29 lip 20:49
Lukas:
2.√x2−2x+1=5−2x
|x−1|=5−2x
1.x∊(−∞,0)
−x+1=5−2x
x=4 ∉D
2.x∊<0,1)
−x+1=5−2x
x=4∉D
3.x∊<1,∞)
x−1=5−2x
3x=6
x=2∊D
29 lip 21:15
Lukas:
3 i 4 już trochę trudniejsze
29 lip 21:18
Eta:
Dlaczego wziąłeś takie przedziały? ?
mają być takie : x∊(−∞, 1) , x∊<1, ∞)
29 lip 21:21
Lukas:
ok. czyli wynik i tak x=2
29 lip 21:23
Eta:
3 i 4 łatwe
− określ dziedzinę
− obustronnie do kwadratu ( bo obydwie strony dodatnie)
− uporządkuj i jeszcze raz obydwie strony do kwadratu
− podaj odp , pamiętając o dziedzinie
powodzenia
29 lip 21:24
Eta:
tak
29 lip 21:24
Lukas:
√x−3+√2x+1=2√x
x−3≥0 i 2x+1≥0 i x≥0
Tak ?
29 lip 21:28
Eta:
No i podaj D: x......
29 lip 21:31
Lukas:
x∊<0,∞)
29 lip 21:32
Eta:
I teraz widzisz,że obydwie strony nieujemne? to możemy ..........
i moje ulubione ....."dokończ"
29 lip 21:34
Eta:
Ejj Lukas ...... nie osłabiaj mnie!
Nie mogę uwierzyć,że nie umiesz wyznaczyć dziedziny! ( część wspólna tych trzech warunków)
Czekam na poprawnie wyznaczoną dziedzinę ........
29 lip 21:36
Lukas:
a jak ustalić dziedzinę w 22:11 ?
√x−3+√2x+1=2√x /2
x−3+2x+1+4√(x−3)(2x+1)=2x
dobrze jak to dej pory?
29 lip 21:37
Lukas:
x≥3
x≥−0,5
x≥0
część wspólna x∊<3,∞)
29 lip 21:39
Eta:
ok
jeszcze nie ma nawet
22oo , więc skąd mam wiedzieć, co napiszesz o
22:11
29 lip 21:40
Eta:
Teraz ok D=<3,∞) lub prosto: x≥3
29 lip 21:41
Eta:
(2√x)2=.................. popraw
29 lip 21:42
Lukas:
pierwszy mój post w tym temacie
29 lip 21:43
Lukas:
x−2+4√(x−3)(2x+1)=4x
29 lip 21:43
Eta:
Teraz uporządkuj i zostaw po lewej stronie wyrażenie 4* pierwiastkiem
napisz co otrzymasz ( tylko be błędów
29 lip 21:45
Saizou :
Etuś mogłabyś tylko sprawdzić mój post z 28 lip 2014 22:50 czy jest tam ok ?
29 lip 21:48
Eta:
Co do wpisu 22:11
tam gdzie trudniej jest określić dziedzinę( a tutaj tak jest)
nie określamy jej, ale po rozwiązaniu sprawdzamy czy równanie jest spełnione
dla wyznaczonego "x" i podajemy właściwą odp.
29 lip 21:49
Eta:
Hej
Saizou jest ok
29 lip 21:50
aaa: Yezoo
ktoś w takie upały czegoś się uczy
mózg się lasuje można tylko zimne
serwować
29 lip 21:50
Eta:
Jak się rozwiązuje zadanka, to mózg się samoistnie schładza
Wypróbuj tę metodę
29 lip 21:52
Saizou : to fajnie, już nie przeszkadzam
Lukasowi w nauce
29 lip 21:52
Lukas:
4
√(x−3)(2x+1)=3x+2 /
2
16(x−3)(2x+1)=9x
2+12x+4
16(2x
2+x−6x−3)=9x
2+12x+4
16(2x
2−5x−3)=9x
2+12x+4
32x
2−80x−48=9x
2+12x+4
23x
2−92x−52=0
Δ=24
√23
29 lip 21:53
Eta:
Wrrrrrrr znów błędy rachunkowe! ( po prawej ........
29 lip 21:55
Eta:
Sprawdź rachunki 21:37 ( to w dodatku : papieska godzina ......
29 lip 21:59
Lukas:
32x2−80x−48=9x2+12x+4
(3x+2)2 mam dobrze przecież ?
29 lip 22:01
Eta:
21:37 sprawdź!
Widzę,że popełniasz dużo błędów rachunkowych, musisz kontrolować dokładnie, to co liczysz.
29 lip 22:03
Lukas:
√x−3+√2x+1=2√x /2
x−3+2x+1+2√(x−3)(2x+1)=4x
3x−2+2√(x−3)(2x+1)=4x
2√(x−3)(2x+1)=2−x /2
4(2x2+x−6x−3)=4−4x+x2
4(2x2−5x−3)=x2−4x+4
8x2−20x−12=x2−4x+4
7x2−16x−16=0
teraz ok ?
29 lip 22:05
Eta:
Skąd wzięła się 4 przed pierwiastkiem po lewej stronie?
29 lip 22:05
Eta:
Wrrrr .........prawa strona w czwartej linijce x+2
29 lip 22:08
Lukas: podniosłem do kwadratu 2√(x−3)(2x+1)
29 lip 22:08
Lukas:
Dziękuję, dziś fatalnie mi idzie, chyba prze upał. Dobranoc i dziękuję ślicznie za pomoc. Jutro
dokończę już bez błędów.
29 lip 22:10
Eta:
21:37 napisałeś 4 przed pierwiastkiem ( czyż nie?
29 lip 22:10
Eta:
Miłych snów
29 lip 22:11
5-latek: Lukas
Ajtek jest bardzo waznym uzytkownikiem tego forum tak jak Panie
Eta
czy
Mila i bardzo pomocnym .
Pewnie jeszce nie raz Ci pomoze . Wiec moze skoncz juz z takim pisaniem . Po prostu , pomijaj
te posty i ich nie czytaj . Dobrze?
29 lip 23:20
Lukas:
3.
√x−3+
√2x+1=2
√x /
2
x−3+3
√(x−3)(2x+1)+2x+1=4x
2
√(x−3)(2x+1)=x+2 /
2
8x
2−20x−12=x
2+4x+4
7x
2−24x−16=0
Δ=1024
√Δ=32
x
2=4∊D
30 lip 18:05
Lukas:
√2−x+√x−1=√x−5
D=x∊<5,∞)
√2−x+√x−1=√x−5 /2
2−x+2√(2−x)(x−1)+x−1=x−5
2√(2−x)(x−1)=x−6 /2
4(−x+2)(x−1)=x2−12x+36
5x2−24x+44=0
Δ<0
brak rozwiązań
30 lip 18:12
razor: 3) dobrze 4) źle dziedzina
30 lip 18:21
Lukas:
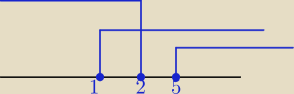
x∊<1,2>suma<5.
∞) ?
30 lip 18:30
Kacper: 2−x≥0 ⇒x≤2
x−1≥0 ⇒ x≥1
x−5≥0 ⇒x≥5
I część wspólna?
30 lip 18:39
Lukas:
zaznaczyłem na wykresie 18:30
30 lip 18:42
Kacper: To jeszcze raz i jeszcze raz... czytaj i myśl
30 lip 18:50
Lukas:
Nie wiem. wydaję się, że dobrze zaznaczyłem ?
30 lip 18:51
Kacper: Dobrze, to doświadczalnie:
Bierz liczbę 5 i sprawdź, czy spełnia wszystkie warunki?
30 lip 18:53
Lukas:
error w pierwszym pierwiastku już jest
30 lip 18:59
razor: x ≤ 2 i x ≥ 5
Czy istnieje jakaś liczba mniejsza od 2 i większa od 5?
30 lip 19:00
Lukas:
a czemu pomijacie warunek x≥1 ?
30 lip 19:30
razor: x ≥ 1 i x ≥ 5 ⇒ x ≥ 5
30 lip 19:32
Lukas:
ok. pomyślę.
30 lip 19:34
Lukas:
x≥5 i x≤2 ?
30 lip 19:37
razor: A jaki jest wynik?
30 lip 19:47
Lukas:
nie widzę tutaj cz.wspólnej
30 lip 19:51
razor: czyli x ∊ ... i wynik równania to...
30 lip 19:52
Lukas:
x∊∅
30 lip 20:00
razor: 
30 lip 20:04
Eta:
30 lip 20:09
Lukas:
Razor w rok da się przygotować do matury R z matematyki ?
30 lip 20:13
razor: Mi się udało w 6 miesięcy zdać na 94%
Jeszcze kilka przykładów do poćwiczenia
1)
√x+1 −
√9−x =
√2x−12
2)
√x2+32 − 2
4√x2+32 = 3
30 lip 20:15
Eta:
Ja odpowiem:
jasne,że się da
Rozwiązuj zadania w "świątek, piątek i niedzielę" i......... będzie 100%na maturze
30 lip 20:17
Lukas:
Rozwiązuję, najgorsze będzie chyba planimetria i bryły. I tak nie idę na studia w tym roku więc
mam dużo czasu.
Przepraszam Eta za moje wcześniejsze komentarze w Twoim kierunku.
| | x2 | |
17+x+2p(17+x)(17−x)+17−x{= |
| |
| | 16 | |
| | x2 | |
2√(17+x)(17−x)= |
| −17 /2 |
| | 16 | |
| | x4 | | 17x | |
4(289−x2)= |
| − |
| +289 |
| | 256 | | 8 | |
| | x4 | | 17x | |
1156−4x2= |
| − |
| +289 |
| | 256 | | 8 | |
dobrze jak do tej pory ?
30 lip 20:22
razor: Błąd w 3 linijce
30 lip 20:25
razor: No i przydałoby się ustalić
dziedzinę
30 lip 20:26
Lukas:
no właśnie 17−x≥0 i 17+x≥0
x≤17 i x≥−17
D=x∊<−17,17>
| | x2 | |
2√(17−x)(17+x)= |
| −34 /2 |
| | 16 | |
| | x4 | | 17x | |
4(17−x)(17+x)= |
| − |
| +1156 |
| | 256 | | 4 | |
| | x4 | | 17x | |
4(289−x2)= |
| − |
| +1156 / *4 |
| | 256 | | 4 | |
| | x4 | |
4624−16x2= |
| −17x+4624 |
| | 64 | |
−1024x
2=x
4−1088
x
4+1024x−1088=0
30 lip 20:41
Eta:
1/ Ustal dziedzinę .............
2/ zanim podniesiesz równanie obustronnie do kwadratu ..... jaka musi być prawa strona?
i teraz podaj zakres x∊...........
30 lip 20:41
razor: w drugiej linijce 17x2 zamiast 17x
30 lip 20:43
Eta:
Nie śpiesz się z drugim podnoszeniem do kwadratu
Najpierw odpowiedz na 2/ pytanie : x∊ ..........
30 lip 20:44
Eta:
No to...... nie przeszkadzam
razorowi
30 lip 20:45
Lukas:
prawa strona nieujemna.
30 lip 20:46
razor: Eta
nie chcę póki co narzucać innego (być może łatwiejszego) sposobu więc niech Lukas zrobi
tak jak chce
30 lip 20:47
Eta:
Ok
( to później podam łatwiejszy sposób rozwiązania tego równania)
30 lip 20:49
Lukas:
x
4+956x
2−294780=0
x
2=t t≥0
t
2+956t−294780=0
Δ
t=2093056
√Δt=64
√511
ale teraz kosmos wychodzi
30 lip 20:57
razor: Gdzieś masz błąd rachunkowy
Powinieneś dojść do postaci x
4 − 64x
2 = 0, lub jeśli nie chce
ci się babrać w rachunkach mogę podać prostszy sposób
30 lip 20:59
Lukas:
Proszę podaj prostszy sposób.
30 lip 20:59
razor: | | x | |
Ustalamy dziedzinę: 17+x ≥ 0 i 17−x ≥ 0 i |
| ≥ 0 |
| | 4 | |
D: x ∊ <0,17>
| | x | |
√17+x + √17−x = |
| | ()2 |
| | 4 | |
| | x2 | |
17+x + 17−x + 2√(17−x)(17+x) = |
| |
| | 16 | |
| | x2 | |
2√(17−x)(17+x) = |
| − 34 |
| | 16 | |
Zanim podniesiemy znowu równanie do kwadratu można zauważyć że lewa strona jest pierwiastkiem,
wobec tego prawa musi być nieujemna
x
2 ≥ 544
Biorąc pod uwagę ustaloną wcześniej dziedzinę x ∊ <0,17> zauważamy że równanie jest sprzeczne
x ∊ ∅
30 lip 21:04
Eta:
30 lip 21:05
Lukas:
x2−544≥0
(x−4√34)(x+4√34)≥0
rozwiązuje tą nierównośc i sprawdzasz czy ma cześć wspólną z dziedziną tak ?
30 lip 21:06
Eta:
Dokładnie tak
30 lip 21:07
Lukas: Chcę jeszcze wrócić do jednego zdania.
√x−3+√2x+1=2√x
x−3≥0 i 2x+1≥0 i x≥0
Tak ?
29 lip 21:28
Eta:
No i podaj D: x......
29 lip 21:31
Lukas:
x∊<0,∞)
29 lip 21:32
Eta:
I teraz widzisz,że obydwie strony nieujemne? to możemy ..........
i moje ulubione ....."dokończ"
a co gdyby dziedzina zacznyła się od liczby ujemnej ? wtedy nie mógłbym podnieś ?
30 lip 21:10
Eta:
Wtedy równanie byłoby sprzeczne ( jak w ostatnim równaniu podanym przez razora
Rozumiesz już, jak to działa?
Jeszcze jedna ważna zasada: jeżeli już znasz sposób rozwiązania zadania,
to pamiętaj ...... kontroluj koniecznie swoje rachunki !
30 lip 21:23
Eta:
@ Lukas
Zad 1(od razora powinieneś już sam rozwiązać
zad2/ wskazówka : podstaw 4√x2+32= t, t≥0 to √x2+32= ....
i dalej już dasz radę
30 lip 21:33
Lukas:
Właśnie już wiem jak rozwiązać
Dziękuję. Mam jeszcze jeden przykład trochę trudniejszy ale
spróbuje sam zrobić
30 lip 21:39
razor: To ja mam jeszcze taki jeden przykład można powiedzieć z gwiazdką
√x−4 + 4√x−8 −
√x−7 + 2√x−8 = 1
tam jest
√x−8 pod pierwiastkiem jak nie widać
30 lip 21:50
Eta:
To ja podam do tego zadania ( z gwiazdką) tylko odp :
x∊<8,∞)
30 lip 22:01
Saizou :
razor nie przesadzaj że z gwiazdką
30 lip 22:06
Lukas:
x−4+4√x−8−x+7−2√x−8=1
3+2√x−8=1
2√x−8=−2
sprzeczne
30 lip 22:08
Saizou :
Lukas] niestety źle
30 lip 22:10
Eta:
@
Lukasa
Zastosuj podstawienie podobnie jak Ci podałam w zad 2/
Dasz radę ......... wierzę w Ciebie
30 lip 22:14
tyu: a ja mam pytanie do tematu, którego uczy się
Lukas, bo robię sobie notatki, a nuż się
przydadzą.
1/ najpierw ustalam dziedzinę, a gdy to jest trudne, to rozwiązuję zadanie metodą analizy
starożytnych − czyli bez dziedziny, a potem sprawdzam rozwiązania, czy równanie jest prawdziwe
2/ Dobrze rozumiem, że obie strony równania mogę podnieść do kwadratu, tylko gdy obie są
nieujemne
(post
Saizou z 28 lipca, godz 22.22 )
30 lip 22:14
Eta:
Dokładnie tak, jak piszesz ... tyu
30 lip 22:16
Saizou :
dokładnie tak np.
2=2 /2
4=4
0=0 /2
0=0
−3=−3
3=3 /2
9=9
ale
−2=2 /2 \
4=4 (z nieprawdy powstała nam prawda)
30 lip 22:17
Eta:
30 lip 22:17
Eta:
Zad. dla
Saizou ( i nie tylko
W czworokącie wypukłym ABCD punkt X jest środkiem boku DC i |∡AXB|=90
o
Wykaż ,że zachodzi |AB|+|BC|≥|AB|
30 lip 22:21
tyu: i teraz pytanie kolejne
(post
Saizou z 28 lipca 22.51) x+
√x+2=10
√x+2=10−x i dać założenie że 10−x≥0,
wtedy te założenie x≤10 ogranicza nam dziedzinę, bo tylko dla x≤10 prawa strona jest nieujemna
30 lip 22:24
razor: tyu zgadza się
Eta chyba źle przepisała
30 lip 22:25
Saizou :
tyu tak (ale to nie kompleta dziedzina, tylko pewnego ograniczenie, wyniki i tak musisz
sprawdzić)
Eta ależ oczywistej jest że |AB|+|BC|≥|AB|→lBCl≥0 xd
30 lip 22:26
tyu: tak, chodziło mi właśnie, że w jakimś stopniu ta dziedzina już jest zawężona, ale nie jest do
końca ustalona.
30 lip 22:28
Eta:
@razor ........co źle przepisałam?
30 lip 22:31
Saizou :
tezę zadanka
30 lip 22:31
Eta:
Hehe
Ma być: |AD|+|BC|≥|AB|
30 lip 22:33
Eta:
No i
Lukas zniechęcił się i...... poszedł wcześniej spać
30 lip 22:37
Saizou :
to mogę ja ^^
30 lip 22:37
tyu: mam jeszcze pytanie do tego założenia 10−x≥0
czy nie można od razu przyjąć, że jeśli √x+2=10−x to 10−x≥0 , bo lewa strona jest pod
pierwiastkiem
Czy może zajść taka sytuacja, że np jeden pierwiastek jest dodatni (arytmetyczny) a drugi
ujemny
np (−3)
2 = 9 i 3
2 =9
30 lip 22:45
Saizou :
właśnie dlatego to przyjmujesz żeby móc podnieść do kwadratu
30 lip 22:46
tyu: coś tam się rozjaśniło w temacie. Dziękuję
30 lip 22:48
Saizou :
zresztą już pisałem że jak tak zrobisz to z nieprawy wyjdzie ci prawda, a tak nie może być xd
30 lip 22:50
Lukas:
Internety mi wyłączyli po prostu
i dlatego nie dokończyłem.
31 lip 17:43
Lukas: a bez podstawienia nie da rady "?
31 lip 21:24
Eta:
Da radę ( ale nieco więcej liczenia
Nie bój się podstawienia .... zobaczysz jak to uprości rachunki
Działaj .............. "dokończ"
31 lip 21:41
Lukas:
tylko nie zawsze wiem jakie podstawienie dać i jakie założenie odnośnie podstawienia.
31 lip 21:42
Saizou :
Eto jakie więcej liczenia xd
√x−4+4√x−8+√x−7+2√x−8=1
√x−8+4√x−8+4+√x−8+2√x−8+1=1 a teraz już z górki xd
31 lip 21:48
Eta:
No to licz
Saizou dalej,skoro "z górki"
31 lip 21:55
Saizou :
√(√x−8+2)2−+
√(√x−8+1)2=1 bo wyżej źle przepisałem
l
√x−8+2l−l
√x−8+1l=1
√x−8+2−
√x−8−1=1
1=1 tożsamość wiec rozwiązaniem jest x∊<8:+
∞), czyli dziedzina równania xd
31 lip 22:02
Eta:
No
31 lip 22:10
Saizou : było z górki xd
31 lip 22:10
Eta:
31 lip 22:11
Eta:
Zapomniałeś w ostatnim o dziedzinie x≥8
31 lip 22:14
Saizou :
no tak, ale w odpowiedzi jest napisane że rozwiązaniem jest dziedzina
31 lip 22:17
Eta:
31 lip 22:17
Eta:
@
Saizou
Jak tam zadanie? które Ci wczoraj podałam
31 lip 22:25
Saizou : szczerze, nie myślałem nad nim
31 lip 22:26
Lukas:
to zaraz porobię z podstawieniem
31 lip 22:33
Lukas:
Już się w tym gubię powoli...
31 lip 22:41
Saizou :
zrób podstawienie √x−8=t , t≥0 i x≥8
31 lip 22:42
Lukas:
nie chodzi o to.
Zrobię wszystkie zdania w tym wątku od początku jeszcze raz. !
31 lip 22:48