Planimetria Blue: W równoległobok, którego przekątne mają długości 10 i 15, wpisano romb w ten sposób, że boki rombu są równoległe do przekątnych równoległoboku. Oblicz długość boku rombu .

Blue: dodam, że tutaj chyba trzeba wykorzystać podobieństwo trójkątów albo twierdzenie Talesa, bo to z tego działu..

bezendu: a=6 tak jest odpowiedź ?

Blue: tak jest, ale powiesz , jak to wyliczyć?

bezendu: https://matematykaszkolna.pl/forum/196184.html

Kacper: W razie pytań proszę pytać

Blue: Kurcze, mógłby to ktoś jakoś wyjaśnić, bo się gubię? Mam tam dwa trójkąty podobne i wyszło mi, że 7,5y = 5 x i co dalej? x=|NP|, y=|DP|

Kacper: za chwilę idę zjeść

Blue: ok Smacznego

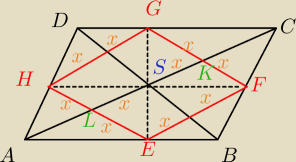
Kacper: dzięki Dobra jestem, to może napiszę jeszcze raz rozwiązanie |AC|=15=a |BD|=10=b |KF|=x − połowa boku rombu dlatego, że kąty FSK oraz LSH są wierzchołkowe, a kąty SFK oraz LHS naprzemianległe. I teraz ponieważ przekątne są równoległe do boków rombu, to mamy podobieństwo trójkątów ΔAHE ~ ΔABD wynika stąd, że:

|AL|		|AS|
	=
|HE|		|BD|

czyli

a   −x 2		a   2
	=
2x		b

	a		a
2x*		=b*(		−x)
	2		2

	a
ax=b*		−bx
	2

	a
ax+bx=b*
	2

	ab
x(a+b)=
	2

	ab
x=
	2(a+b)

	ab
2x=
	a+b

Gotowe

Kacper: Zastanów się jak pokazać, że przekątne równoległoboku i rombu przecinają się w tym samym punkcie

Blue: Dzięki hm... ale nie wiem za bardzo, jak to udowodnić i powiedz mi proszę skąd wiemy, że |SL| ma długość x?

nikt:

	1
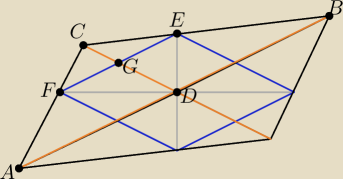
|AB| = 15. |CD| = 5, |DG| =		|EF|
	2

|EF|		1   |CD| − |EF|   2
	=
|AB		|CD|

	|AB| * |CD|
|EF| =
	1   |CD| + |AB|   2

	15 * 5
|EF| =
	5 + 7,5

Kacper: przeczytaj uzasadnienie po słowie dlatego

nikt: A gdzie jest "dlatego"?. Ty Kacper tez nie możesz oprzeć się urokowi iksa, a mówili, że jesteś na iksa odporny

Eta: Długość boku tego rombu]] to połowa średniej harmonicznej długości przekątnych równoległoboku

Kacper: Było początkowo "c", ale się ten iks przyplątał