macierz
Paulina:
Jak policzyć wyznacznik macierzy (stosując rozwinięcie Laplac'a ) ?
|3 3 4 −5 |
|5 −7 8 2 |
|4 5 −7 −3|
|7 8 2 4|
1 sie 18:46
Paulina: ?
1 sie 19:24
1 sie 20:09
Paulina:
jak byś zauważył to w linku masz prosty przykład... gdzie jest 1 wtedy łatwo wyzerować kolumnę
czy wiersz tutaj jej nie ma więc może zapoznaj się z teorią której nie znasz a potem podsyłaj
mi link...
1 sie 20:22
Kacper: Dlaczego jesteś taka niemiła?
Równie dobrze to samo mogę powiedzieć o tobie, poczytaj teorię, a będziesz wszystko wiedzieć

Nikt nie karze ci w rozwinięciu Laplace'a zerować kolumny lub wiersza.
Jak koniecznie chcesz uzyskać zera to można mnożyć wiersze i kolumny przez stałe (tylko
wyznacznik się zmienia wtedy)
1 sie 20:32
Paulina:
Jak bym nie znała teorii to bym nie wstawiała tego zadania.. Dwa w linku jest banalny przykład
który nijak ma się do mojego zapytania. Trzy muszę zrobić to za pomocą rozwinięcia Laplace'a a
nie eliminacją Gaussa..
1 sie 20:37
Kacper: To wybierasz wiersz lub kolumnę i rozwijasz

Np względem pierwszej kolumny:
detA=(−1)
1+1*3*detA
11+(−1)
2+1*5*detA
21+
+(−1)
3+1*4*detA
31+(−1)
4+1*7*detA
41
1 sie 20:42
Paulina:
Tego nie znałam.
Widziałem że mnoży się kolumny albo wiersze przez jakąś liczbę i wtedy ładnie się zeruję,
najlepiej jak jest jedynka

1 sie 20:47
Godzio:
Dlatego trzeba sobie upraszczać. Zacznę, Ty dokończysz...
3 3 4 −5 w1
5 −7 8 2 w2
4 5 −7 −3 w3
7 8 2 4 w4
w4 − 2w1
w3 − w1
3 3 4 −5
5 −7 8 2
1 2 −11 2
1 2 −6 14
w1 − 3w4
w2 − 5w4
w3 − w2
0 −3 22 47
0 −17 38 −68
0 0 −5 −12
1 2 −6 14
Wyznacznik tej macierzy jest równy wyznacznikowi macierzy:
−3 22 47
−17 38 −68
0 −5 −12
Teraz proponuję:
w2 − 6w1
i później w1 − w2 i znów Laplacem, wyznacznik macierzy 2x2 już wiadomo jak liczyć
1 sie 21:22
Kacper: Można i tak

Trzeba policzyć kilka przykładów, żeby wprawy nabrać

1 sie 21:31
Gustlik: Godzio, jak już masz wyznacznik 3 stopnia, to łatwiej Sarrusem niż Laplace'm.
2 sie 00:40
Godzio:
Nie zawsze, czasem jedno działanie znacznie upraszcza

(w tym wypadu, przy dużych liczbach
trudność będzie podobna

)
2 sie 00:51
Paulina:
Dzięki, nie wiedziałam, że takie triki są

2 sie 17:25
Paulina:
możecie podać jeszcze jakiś przykład macierzy ?
3 sie 11:11
Kacper: np taki:
1 2 2 3
1 0 −2 0
3 −1 1 −2
4 −3 0 2
i druga:
4 5 1 2
1 −7 5 −3
−4 9 2 1
3 2 5 7
Wymyślić można bardzo łatwo

i jeszcze jeden

2 3 5 7
−1 3 4 2
−8 −9 −15 −21
4 7 11 9
3 sie 11:25
Paulina:
Te są proste bo są 1

chodzi o takie gdzie nie od razu widać rozwiązanie

3 sie 13:06
Godzio:
To daj sobie zamiast 1 dowolne liczby

3 sie 13:27
Paulina:
3 4 5 6 w1
2 2 2 2 w2
9 9 8 7 w3
2 3 4 7 w4
w1−w2
w2*(−1)+w4
w1*(−3)+w3
Mogę tak ?
3 sie 13:43
Paulina: ?
3 sie 14:17
3 sie 20:44
Paulina: ?
3 sie 21:43
Paulina: No one?

3 sie 21:54
Mila:
Metodą Godzia masz wynik 6095 czy za pomoca kalkulatora?
3 sie 22:28
Paulina:
Za pomocą kalkulatora
3 sie 22:30
Mila:
Z czym masz problem, co Ci nie wychodzi w wyznaczniku macierzy z 18:46?
3 sie 22:32
Paulina:
Godzio napisał, że to taki sam wyznacznik a tutaj inne wyznaczniki wgl wychodzą.
Nie wiem jak za pomocą rozwinięcia LaPlace'a policzyć ten wyznacznik macierzy.
Wiem, że muszę wyzerować kolumnę albo wiersz i potem z reguły Sarrusa policzyć wyznacznik
macierzy 3x3.
Ale problem jest taki, że w macierzy nie ma żadnej 1, żeby to ładnie się wszystko redukowało.
3 sie 22:36
Godzio:
Może się walnąłem w dodawaniu, człowiek nie jest istotą doskonałą i mylić się też może, ja
tylko zademonstrowałem metodę

3 sie 22:37
Godzio:
Już widzę 1 błąd, nie dałem minusa, powinno być w pierwszym wierszu − 47, a druga rzecz, przy
rozwinięciu (wtedy o tym pamiętałem, ale nie napisałem tego) trzeba dać minus przed całym
wyznacznikiem, bo pozycja 1 jest nieparzysta (4 wiersz + 1 kolumna = 5)
3 sie 22:40
Godzio: |−3 22 −47 |
− |−17 38 −68|
|0 −5 −12 |
Ten wyznacznik powinniśmy otrzymać (już po wszystkich operacjach)
3 sie 22:42
Paulina:
a post 13:43 ?
3 sie 22:42
Paulina:
Teraz jest ok.
3 sie 22:44
Godzio:
Teoretycznie możesz, ale pokaż co Ci z tego wyjdzie, bo wykonując pewne operacje nie możesz
korzystać ze starych i nowych wierszy jednocześnie (a właściwie możesz, ale trzeb to
umiejętnie zrobić

)
3 sie 22:50
Mila:
Macierz Godzia ma jedną pomyłkę ma być (−47) i wychodzi ładnie . Łatwo sie w tym pomylić.
Możesz zrobić inaczej , wydaje mi się łatwiej.
3 3 4 −5
5 −7 8 2
4 5 −7 −3
7 8 2 4 Od pierwszej kolumny odejmuję drugą.
0 3 4 −5
12 −7 8 2
−1 5 −7 −3
−1 8 2 4 od czwartego wiersza odejmuję trzeci wiersz
0 3 4 −5
12 −7 8 2
−1 5 −7 −3
0 3 9 7 od czartego wiersza odejmuję pierwszy wiersz
0 3 4 −5
12 −7 8 2
−1 5 −7 −3
0 0 5 12
Już liczę wyznacznik
(−1)4+1*0*[...] + (−1)4+2*0*[...]+ tu wyjdą zera
(−1)4+3*5*[ 0 3 −5
12 −7 2
−1 −5 −3 ] licz metodą Sarrusa
+(−1)4+4*12* [0 4 4
12 −7 8
−1 5 −7] licz metodą Sarrusa
Chyba się nie pomyliłam w przepisywaniu z kartki.
det(A)=6095
3 sie 22:59
Paulina:
ale chyba coś nie tak ?
Skoro zerujesz wiersz to działasz na kolumnach a skoro kolumnę to działasz na wierszach
Godzio to jak można ?
3 sie 23:01
Godzio:
Zależy co chcesz zerować, można i tak i tak.
3 sie 23:03
Paulina:
jeżeli chcę zerować wiersz to nie mogę dodawać wierszy do siebie tylko muszę dodawać/odejomować
kolumny. ?
3 sie 23:06
Godzio:
Pewnie przez operacje na wierszach też coś by się dało, ale ciężko

3 sie 23:09
Paulina:
Chciałam się tego naumieć przed październikiem ale słabo mi to idzie. w średniej matma to była
bajka w porównaniu do tych całek i różniczek o wgl

3 sie 23:11
Mila:
To może lepiej nie mieszać, ale obliczyłaś to co Godzio podał na końcu?
3 sie 23:17
Paulina:
To obliczyłam.
3 sie 23:18
Mila:
Wg mojego algorytmu też?
Jutro popatrzę do teorii, bo to mi już zardzewiało. Godzio jest na bieżąco.
To potwiedzę albo odwołam.
3 sie 23:52
4 sie 00:09
Mila:
Nie musisz przecież przekształcać macierzy, jeśli to Ci sprawia trudność , rozwijaj wg
najprostszego wg Ciebie wiersza (kolumny) i wyznacznik macierzy 3x3 umiesz przeciez
liczyć.Będziesz miała więcej liczenia ale cel osiągniesz.
4 sie 00:12
Kacper: Po południu będę miał trochę czasu to wrzucę kilka przykładów jeszcze

4 sie 09:22
Paulina:
Dziękuję.
Mila ale chodzi o to, że w poleceniu mam korzystać z rozwinięcia LaPlace'a inaczej wgl bym
liczyła Gaussem ale nie można.
4 sie 10:28
Mila:
To nie wiem z czym masz problem, czy w obliczaniu wyznacznika metodą L. czy doprowadzeniem
macierzy do dogodnej postaci?
4 sie 15:42
Paulina:
w doprowadzeniu macierzy do postaci 3x3
4 sie 15:43
Mila:
W wyzerowaniu w macierzy 4X4 trzech wyrazów kolumny albo 3 wyrazów wiersza?
To podaj zadanie, będziemy ćwiczyc.
4 sie 15:50
Paulina:
Tak, dokładnie tak:
korzystając z rozwinięcia Laplace'a znajdź wyznacznik macierzy
a)
9 3 2 2
7 3 2 0
2 2 3 9
7 5 7 7
4 sie 15:58
Mila:
1)od drugiego wiersza odejmij pierwszy
4 sie 16:09
Paulina:
9 3 2 2
−2 0 0 −2
2 2 3 9
7 5 7 7
?
4 sie 16:16
Mila:
Na razie wyłączam komputer, bo jest burza, możesz już liczyć wyznacznik wg drugiego wiersza.
4 sie 16:19
Paulina:
Nie bardzo wiem jak... Będę czekać.
4 sie 16:21
J:
3 2 2 9 3 2
det (A) = −2*(−1)3 2 3 9 + 0 + 0 − 2*(−1)6 2 2 3 = .......
5 7 7 7 5 7
4 sie 16:40
Mila:
Masz podpowiedź od J, to licz,ma być wynik (−140).
4 sie 16:59
Paulina:
ale nie rozumiem tego zapisu..
Chodzi o to jak krok po kroku zerować wiersze i kolumny żeby otrzymać macierz 3x3.
4 sie 17:03
Kacper: Chyba wiem czego nie rozumiesz

Wiesz skąd się wzięły poszczególne macierze 3x3?
4 sie 17:04
Paulina:
właśnie nie.
4 sie 17:05
J:
3 2 2
Skreślasz 1 kolumne i drugi wiersz: dostajesz: 2 3 9
5 7 7
9 3 2
Skreslasz 4 kolumne i drugi wiersz: dostajesz: 2 2 3
7 5 7
................ i wynik taki ,jak podaje Mila ... − 140
4 sie 17:12
Kacper:
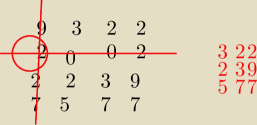
Dobra to zrobię ci ładny rysunek

Patrzymy na drugi wiersz i będziemy stosować rozwinięcie Laplace'a właśnie względem niego
Wzór jest taki
detA=∑(−1)
i+ja
ij*detA
*ij
Ostatnią macierz różnie się oznacza
Zaczynamy od liczby −2, i nasz wzór ma postać:
(−1)
2+1*(−2)*detA
*21
teraz wytłumaczenie jak powstaje macierz A*
21 (patrz rysunek wyżej

)
Powstaje ona przez skreślenie wiersza i kolumny w której stoi dany wyraz macierzy.
Mam nadzieję, że teraz wiadomo o co chodzi

4 sie 17:14
Paulina:
ale żeby skreślić wiersz to nie muszą być tam 3 zera i element niezerowy ?
4 sie 17:18
J:
Krótko mówiąc , po skreśleniu danego wiersza i kolumny przepisujesz to, co pozostało,
tak jak narysował
Kacper .

4 sie 17:18
J: Nie ... dlatego też masz we wzorze,który Ci napisałem 0 + 0 ( bo te iloczyny się wyzerują )
4 sie 17:20
J:
Dletego Mila zasugerowała Ci liczyć wg drugiego wiersza bo tam są az dwa zera.
4 sie 17:21
Mila:
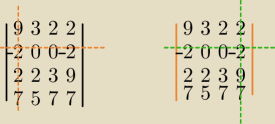
Ponieważ nie nasuwa mi się szybko sposób wyzerowania trzeciego wyrazu w 2 wierszu to już
rozwijam wg drugiego wiersza.
Po kolei : (−1)
2+1 bo (−2) jest w drugim wierszu i pierwszej kolumnie.
Wykreślam drugi wiersz i pierwszą kolumnę zostaje macierz 3X3
(−1)
2+1*(−2) *| 3 2 2|
| 2 3 9|
| 5 7 7|
+(−1)
2+2*0 * [...] +(−1)
2+3*0*[...]+
+(−1)
2+4*(−2)*[ 9 3 2]
[2 2 3]
[7 5 7]
Teraz dokończysz?
4 sie 17:21
J:
3 0 0 0 8 9 7
gdybyś miała np : 5 8 9 7 , to : det(A) = 3*(−1)2* 8 2 6 + 0 + 0 + 0
4 8 2 6 5 5 5
7 5 5 5
4 sie 17:24
Paulina:
Dziękuję.
teraz już nie mam problemu z macierzą 3x3. Najgorsze jest dla mnie właśnie to przejście na
macierz 3x3 a dalej to już pikuś

4 sie 18:03
Mila:
Daj następną macierz i załącz obliczenia.
4 sie 18:25
Paulina:
b) 9 9 −2 −4
2 3 9 0
0 −5 −5 −5
2 2 −2 3
1) w4*(1)
2) w1+w4
4 sie 18:59
asdf: pamietam te liczenie wyznacznikow macierzy...bylo to takie...nudne

dobrze, ze nie musze juz
do tego wracac

Wedlug mnie lepiej sie wziac za granice, pochodne i jak sie zdarzy − calki.
4 sie 19:40
Mila:
9 9 −2 −4
2 3 9 0
0 −5 −5 −5
2 2 −2 3
k1−k2
0 9 −2 −4
−1 3 9 0
5 −5 −5 −5
0 2 −2 3
k2+k3
0 7 −2 −4
−1 12 9 0
5 −10 −5 −5
0 0 −2 3
Teraz rozwiń na dwa sposoby
4 sie 20:25
Mila:
Masz rację asdf, nudne, ale cóż robić, trzeba się nauczyć.
4 sie 20:27
Paulina:
Teraz mając tą ostatnią macierz
skreślam pierwszą kolumnę i 4 wiersz tak ?
4 sie 20:39
Kacper: Zależy względem którego wiersza rozwijasz lub kolumny

4 sie 20:40
Paulina:
O Boże... nie wiem.. po prostu chcę wykreślić jedną kolumnę i jeden wiersz.
7 −2 −4
12 9 0
−10 −5 −5
detA=....
4 sie 20:46
Mila:
Albo tak:
9 9 −2 −4
2 3 9 0
0 −5 −5 −5
2 2 −2 3
k2−k3
9 11 −2 −4
2 −6 9 0
0 0 −5 −5
2 4 −2 3
k3−k4
9 11 2 −4
2 −6 9 0
0 0 0 −5
2 4 −5 3
4 sie 20:50
Paulina:
to wtedy już nie będzie problemu
bo mam −5*(−1)4+3=−5*|9 11 2 |
|2 −6 9 |
|2 4 −5|
4 sie 20:53
Mila:
Napisz sobie na kartce:
Wg 4 wiersza 20:25
1) 4 wiersz i 3 kolumna
+
2) 4 wiersz , 4 kolumna
Teraz tu napisz
4 sie 20:54
Mila:
20:53 dobrze, podaj wynik.
I poprzednią wersję musisz tez umieć, to wreszcie zrozumiesz.
4 sie 20:56
Paulina:
detA=−1470
4 sie 21:03
Paulina:
Dziękuję jutro wrócę do tego bo dziś teraz burza u mnie.
Ogólnie to będę dwa kierunki studiować

4 sie 21:04
Mila:
(−1)*(−5)=5
W=1470
4 sie 21:10
PW: Tak sobie od 2 dni czytam ten wątek i jako stary złośliwy dziad muszę skomentować.
Paulino, polecenie "policz wyznacznik stosując rozwinięcie Laplace'a" należy wykonać
dosłownie − rozwijać względem wiersza (lub kolumny) i robić tak dotąd, aż występujące w
rozwinięciu wyznaczniki dadzą się policzyć wprost z definicji. Metis miał rację.
Korzystanie z jakiegoś "zerowania" wierszy czy kolumn to zupełnie inna bajka (inne
twierdzenie, którego nie nazywa się rozwinięciem Laplace'a).
To co chciałaś, i co wymusiłaś na kolegach podpowiadających, może być stosowane, gdy polecenie
brzmi "oblicz wyznacznik" − wtedy wszystkie chwyty dozwolone. Twoje komentarze z 1 sierpnia o
20:22 i 20:37 świadczą właśnie o niezrozumieniu teorii. Nie przyswoiłaś dokładnie treści
twierdzeń, lecz dążysz do tego "jak to się robi".
4 sie 21:47
mietek: Rozwinięcie Laplace'a nie polega na zerowaniu wierszy i kolumn macierzy. Kiedy wy to wreszcie
zrozumiecie?
4 sie 22:14
Mila:
Czy Ty rozumiesz, że w pierwszej linijce jest pytanie "jak policzyć wyznacznik macierzy 4x4"?.
Może nie umiem tyle z matematyki co Ty mietku, ale nie wyzłośliwiam się w stosunku do
innych forumowiczów, a błędy swoje poprawiam, jeśli zauważę.
4 sie 22:20
asdf: mietek, chcesz sie czepiac to nie to miejsce. Tutaj kazdy sie uczy od kazdego, a nie sie go
czepia o glupie slowka. Z tego co jest napisane na wikipedii:
wzór rekurencyjny określający wyznacznik n−tego stopnia macierzy kwadratowej o wymiarach n
x n.
A jak wygladaja obliczenia − pewnie wiesz...wiec sie nie czepiaj i nara.
4 sie 22:48
Mila:
4 sie 23:38
Paulina:
Mietek to typowy troll który nic nie potrafi a czepia się wszystkiego... Wystarczy kliknąć w
jego nick i zobaczyć, że nie rozwiązał żadnego zadania.. To po prostu jakieś dziecko które
musi się dowartościować...
5 sie 15:24
Paulina: @PW w takim razie jak nazywa się ''proces'' zerowania całej kolumny lub wiersza ?
5 sie 20:56
Mila:
Przed zastosowaniem rozwinięcia Laplace'a do obliczenia wartości wyznacznika przekształcamy
macierz , aby ułatwić sobie obliczenia. To nie jest konieczne. Tak przekształcamy aby nie
zmienić wartości wyznacznika i wyzerować część wiersza albo kolumny, nie możesz wyzerować
całej kolumny, poczytaj o własnościach wyznaczników.
http://www.youtube.com/watch?v=LUnQDKxse4E
5 sie 21:36
PW: Nie ma czegoś takiego − procesu, który prowadzi do zerowania całej kolumny lub wiersza. Może to
się udać w szczególnym wypadku − gdy kolumny (wiersze) macierzy tworzą układ liniowo zależny,
wtedy wyznacznik ma wartość zero.
To co się dla wygody robi, czyli dodawanie do kolumny macierzy innej kolumny pomnożonej przez
dowolną liczbę (co nie zmienia wartości wyznacznika) chyba nie ma specjalnej nazwy, bywa
określane jako wykonywanie elementarnych operacji na kolumnach wyznacznika.
5 sie 21:57
Paulina:
Dziękuję. Poczytam o tym.
@PW nie chodziło mi o zerowanie całej kolumny lub wiersza tylko o zostawienie jednego elementu
niezerowego w kolumnie lub wierszu.
6 sie 18:49
Mila:
Widzę, że zniechęciłaś się, albo już opanowałaś problem.
6 sie 21:02
Paulina:
Witaj Mila.. Bardziej to drugie.Muszę zająć się dzieckiem siostry i nie mam za bardzo czasu
żeby robić zadania. Ale już niedługo wrócę do tego

Pozdrawiam

7 sie 15:47
Mila:

7 sie 18:54
Paulina:
Chcę wrócić do tego co napisał Godzio :
Teoretycznie możesz, ale pokaż co Ci z tego wyjdzie, bo wykonując pewne operacje nie możesz
korzystać ze starych i nowych wierszy jednocześnie (a właściwie możesz, ale trzeb to
umiejętnie zrobić
o co mu dokładnie chodziło ?
16 sie 18:08
16 sie 18:48
 Nikt nie karze ci w rozwinięciu Laplace'a zerować kolumny lub wiersza.
Jak koniecznie chcesz uzyskać zera to można mnożyć wiersze i kolumny przez stałe (tylko
wyznacznik się zmienia wtedy)
Nikt nie karze ci w rozwinięciu Laplace'a zerować kolumny lub wiersza.
Jak koniecznie chcesz uzyskać zera to można mnożyć wiersze i kolumny przez stałe (tylko
wyznacznik się zmienia wtedy)
 Np względem pierwszej kolumny:
detA=(−1)1+1*3*detA11+(−1)2+1*5*detA21+
+(−1)3+1*4*detA31+(−1)4+1*7*detA41
Np względem pierwszej kolumny:
detA=(−1)1+1*3*detA11+(−1)2+1*5*detA21+
+(−1)3+1*4*detA31+(−1)4+1*7*detA41

 Trzeba policzyć kilka przykładów, żeby wprawy nabrać
Trzeba policzyć kilka przykładów, żeby wprawy nabrać 
 (w tym wypadu, przy dużych liczbach
trudność będzie podobna
(w tym wypadu, przy dużych liczbach
trudność będzie podobna  )
)

 i jeszcze jeden
i jeszcze jeden  2 3 5 7
−1 3 4 2
−8 −9 −15 −21
4 7 11 9
2 3 5 7
−1 3 4 2
−8 −9 −15 −21
4 7 11 9
 chodzi o takie gdzie nie od razu widać rozwiązanie
chodzi o takie gdzie nie od razu widać rozwiązanie 



 )
)



 Wiesz skąd się wzięły poszczególne macierze 3x3?
Wiesz skąd się wzięły poszczególne macierze 3x3?
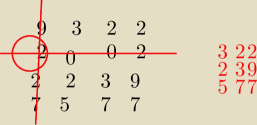 Dobra to zrobię ci ładny rysunek
Dobra to zrobię ci ładny rysunek  Patrzymy na drugi wiersz i będziemy stosować rozwinięcie Laplace'a właśnie względem niego
Wzór jest taki
detA=∑(−1)i+jaij*detA*ij
Ostatnią macierz różnie się oznacza
Zaczynamy od liczby −2, i nasz wzór ma postać:
(−1)2+1*(−2)*detA*21
teraz wytłumaczenie jak powstaje macierz A*21 (patrz rysunek wyżej
Patrzymy na drugi wiersz i będziemy stosować rozwinięcie Laplace'a właśnie względem niego
Wzór jest taki
detA=∑(−1)i+jaij*detA*ij
Ostatnią macierz różnie się oznacza
Zaczynamy od liczby −2, i nasz wzór ma postać:
(−1)2+1*(−2)*detA*21
teraz wytłumaczenie jak powstaje macierz A*21 (patrz rysunek wyżej  )
Powstaje ona przez skreślenie wiersza i kolumny w której stoi dany wyraz macierzy.
Mam nadzieję, że teraz wiadomo o co chodzi
)
Powstaje ona przez skreślenie wiersza i kolumny w której stoi dany wyraz macierzy.
Mam nadzieję, że teraz wiadomo o co chodzi 

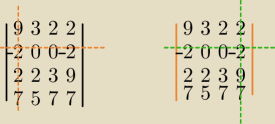 Ponieważ nie nasuwa mi się szybko sposób wyzerowania trzeciego wyrazu w 2 wierszu to już
rozwijam wg drugiego wiersza.
Po kolei : (−1)2+1 bo (−2) jest w drugim wierszu i pierwszej kolumnie.
Wykreślam drugi wiersz i pierwszą kolumnę zostaje macierz 3X3
(−1)2+1*(−2) *| 3 2 2|
| 2 3 9|
| 5 7 7|
+(−1)2+2*0 * [...] +(−1)2+3*0*[...]+
+(−1)2+4*(−2)*[ 9 3 2]
[2 2 3]
[7 5 7]
Teraz dokończysz?
Ponieważ nie nasuwa mi się szybko sposób wyzerowania trzeciego wyrazu w 2 wierszu to już
rozwijam wg drugiego wiersza.
Po kolei : (−1)2+1 bo (−2) jest w drugim wierszu i pierwszej kolumnie.
Wykreślam drugi wiersz i pierwszą kolumnę zostaje macierz 3X3
(−1)2+1*(−2) *| 3 2 2|
| 2 3 9|
| 5 7 7|
+(−1)2+2*0 * [...] +(−1)2+3*0*[...]+
+(−1)2+4*(−2)*[ 9 3 2]
[2 2 3]
[7 5 7]
Teraz dokończysz?

 dobrze, ze nie musze juz
do tego wracac
dobrze, ze nie musze juz
do tego wracac  Wedlug mnie lepiej sie wziac za granice, pochodne i jak sie zdarzy − calki.
Wedlug mnie lepiej sie wziac za granice, pochodne i jak sie zdarzy − calki.


 Pozdrawiam
Pozdrawiam 
