trygonometria tyu: czy ktoś mógłby mi wytłumaczyć o co chodzi z takim rozwiązaniem

	1
x=α0+kπ, gdzie ctgα0=
	2

to jest jeden z wyników do takiego przykładu cos²x − 3 sin x cos x + 1 = 0 link https://matematykaszkolna.pl/forum/155605.html nie wiem co oznacza ten kąt α₀

Eta: α_o −− to taki kąt dla którego ctgα_o=0,5 ⇒α_o≈ 64^o W rozwiązaniu równania nie podajemy przybliżonych wartości kąta dlatego piszemy: x= α_o+kπ, gdzie ctgα_o=0,5

	π
Jeżeli miałbyś ctgαo=√3 ⇒ αo=
	6

	π
wtedy piszemy odp: x=		+kπ
	6

Czy teraz już jasne?

tyu: tak. Dziękuję.

Eta:

Godzio:

	1
Zawsze możemy napisać arcctg(		) + kπ
	2

tyu: jeśli tak mówisz Może ktoś mógłby mi wytłumaczyć dlaczego cos²x=0 Skorzystałem sobie z wykresu i wiem jak to wygląda, ale nie wiem dlaczego tak się dzieje, że wykres cosx "odbija" się od OX

tyu: ktokolwiek

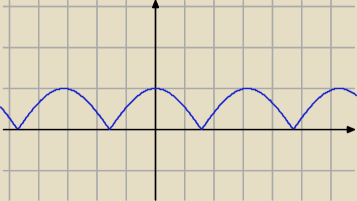
Saizou : bo

	π		π
cosx ≥0 dla x∊[−		+2kπ:		+2kπ]
	2		2

	π		3
cosx≤ dla x∊(		+2kπ;		π+2kπ)
	2		2

a wiemy że { x , x≥0 lxl={ { −x, x<0 zatem... cosx , cos≥0 lcosxl= − cosx, cos<0 albo inaczej mówiąc moduł mówi nam o tym że to co pod osią OX odbija się symetrycznie nad oś OX

tyu: dzięki Saizou, ale dzisiaj już tego nie zrozumiem. Jutro do tego wrócę

Saizou : najważniejsze jest ostatnie zdanie (tak dla intuicji)

tyu: rozumiem ten moduł z cosx, ale co on ma wspólnego z cos²x

razor: Pomógłbym ale nie wiem o co pytasz

tyu: Saizou rozpisał ten moduł, ale nie wiem jaki związek istnieje pomiędzy modułem z coxx a rówananiem cos²x=0

razor: Równanie cos²x = 0 ma takie same rozwiązania jak równanie cosx = 0 które raczej potrafisz rozwiązać

J: Saizou narysował Ci po prostu wykres funkcji: y = IcosxI ... i nie ma to nic wspólnego z cos²x = 0

tyu: no to jakie jest uzasadnienie, że cos²x=0 ma wykres taki jak ma, czyli to co pod OX jest nad OX. Próbowałem to sobie jakoś rozpisać, że cos²x= cosx * cosx i ZW cosx to <−1;1> ale wynika z tego żaden wniosek

razor: ()² ≥ 0 dla każdego Poza tym cos²x i |cosx| mają różne wykresy

Saizou : może chodzi o to, że cos²x=0 /√ √cos²x=0 wiemy że √a²=lal lcosxl=0

tyu: te wykresy się różnią trochę przy osi OX

razor: Wykresy się różnią ale rozwiązanie równania jest takie same

J: Problem polega na tym,że tyu zadał naraz 2 pytania i trzeba mu odpowiedzieć na każde osobno. (post:23:37) "Może ktoś mógłby mi wytłumaczyć dlaczego cos2x=0 Skorzystałem sobie z wykresu i wiem jak to wygląda, ale nie wiem dlaczego tak się dzieje, że wykres cosx "odbija" się od OX" 1) Na pytanie 1 już sobie sam odpowiedział , ale błędnie. Wykres y = cos²x nie ma żadnego odbicia. 2) Natomiast aby narysować wykres y = IcosI trzeba wykres y = cosx odbić względem osi OX. ( tak się robi w przypadku każdego wykresu: y = If(x)I )

Saizou : niebieski to lcos(x)l czerwony to cos(x), a zielone kropki to rozwiązania xd

Kacper:

	1
cos2x=cos2x−sin2x=cos2x−(1−cos2x)=2cos2x−1 ⇒cos2x=		(cos2x+1)
	2

Teraz można wykonać wykres przy pomocy przekształceń funkcji f(x)=cosx

tyu: Kacper, ale Ty rozpisałeś mi cos2x, a mi chodzi o cos²x.. najbardziej chyba jasne jest to wytłumaczenie, które przedstawił razor czyli x²≥0 dla każdego x

Saizou : dla każdego x ∊ R (ściślej ujmując)

tyu: dziękuję za pomoc.

Kacper: tyu ja napisałem ci jak narysować wykres f(x)=cos²x

tyu: no tak, końcówka równania. Nie doczytałem. Dzięki