wzór na obliczanie odległości od punktu (x,y) do odcinka tomker: Chcę poznać wzór na obliczanie odległości od punktu (x,y) do odcinka o współrzędnych (x1, y1) i (x2, y2). Generalnie chodzi o znalezienie najkrótszej drogi od tego punktu do tego konkretnego ODCINKA (NIE PROSTEJ)

Ajtek: saizou dajesz

Saizou : Ajtek zostawię Tobie, bo obecnie jestem bombardowany na fb xd

Ajtek: Cfaniaczek, wróciłem po długiej nieobecności i wszystko na mnie .

Saizou : ale ogólnie −ułożyć prostą AB −ułożyć proste prostopadłe przechodzące przez punkty A oraz B −rozpatrzeć przypadek kiedy P leży między prostymi prostopadłymi (wtedy liczysz odległość punktu od prostej AB) − rozpatrzeć kiedy P jest bliżej punktu A lub B (wtedy jest to zwykła odległośc między punktami)

tomker: Wy tak zawsze?

Ajtek: Tzn? Czy my zawsze spamimy w wątkach?

tomker: tak

Ajtek: Jeśli jest możliwość i czas to owszem .

PW: Gotowego wzoru nie ma − odległość punktu P od zbioru Z to kres dolny odległości od P do Q, gdzie Q∊Z.

Saizou : ale masz receptę to do dzieła xd

Ajtek: Cześć PW .

Saizou : oooo... cześć PW, Ciebie też nie było jakiś czas xd

Ajtek: Noc powrotów, czy jak

Metis: PW wyleczony?

tomker: Jakaś podpowiedź łopatologiczna. Idiota nie jestem, ale matematykiem też nie.

Saizou : tomker będe liczył na kartce jak się dolicze to przepiszę xd

Ajtek: Saizou, to klep rozwiązanie tutaj na bieżąco, szkoda czasu

PW: Operacja się udała, pacjent przeżył. I tak nie widzę dobrze, bo najpierw robią "gorsze" oko. Starość to piękny okres w życiu człowieka pod warunkiem, że jest się zdrowym i bogatym.

Saizou : nie po musze przełączać między kartami

Ajtek: Oj PW, nie wiedziałem, że masz problemy ze zdrowiem. Zatem zdrowia życzę i miło Ciebie na forum widzieć !

PW: Dziękuję za miłe słowa. A jeżeli się nudzicie, to może zajmiecie się układaniem kafelków 255447. Ładne zadanie − umiałbym je rozwiązać przy pomocy komputera, ale jak to wyliczyć "ręcznie"?

Saizou : chyba jednak dzisiaj jest za późno na liczenie tego, bo mi się już indeksy mylą, zatem jak wstanę to się pomęczę xd

tomker: Byłbym Ci wdzięczny

jakubs: Zdrowia PW !

Metis: PW>matematyka.pisz.pl/forum/255193.html Trochę uciekl ten post

Ajtek: Wracając do zadania. Czy nie wystarczy znaleźć punktu przecięcia się prostych prostopadłych: zawierających odcinek AB i prostej przechodzącej przez P? Następnie wyciągnięcie wniosku? To jest kres dolny jak pisze PW. Tylko, czy kres dolny to szkoła średnia?

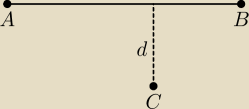
Gotowiec: Jest gotowy wzór. A = (x₁, y₁), B = (x₂, y₂), C = (x₀, y₀)

	|x0(y2 − y1) + y0(x1 − x2) + x2y1 − x1y2|
d =
	√(x2 − x1)2 + (y2 − y1)2

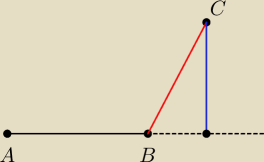
Ajtek: Czy ten wzór zadziała w tym przypadku Gotowiec?

hanka: Co to jest odległość w kontekście warunków tego zadania?

tomker: hanka: Odległość, czyli długość odcinka. Chcę poznać długość odcinka CB

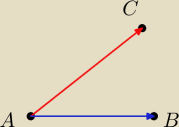
MQ: Bardzo łatwo z rachunku wektorowego: Liczysz rzut wektora AC^→na wektor AB^→:

	AC→◯AB→
w→=		AB→
	|AB→|2

	AC→◯AB→
a dokładniej tylko współczynnik
	|AB→|2

	AC→◯AB→
Jeżeli		∊(0,1), to najmniejszą odległość liczysz ze wzoru podanego przez
	|AB→|2

Gotowca

	AC→◯AB→
Jeżeli		<0, to bierzesz odległość AC
	|AB→|2

	AC→◯AB→
Jeżeli		>1, to bierzesz odległość BC
	|AB→|2

MQ: Miało być ≤ i ≥ w odpowiednich nierównościach.

tomker: Rozumiem, ale co oznacza ◯ Abo inaczej, jak ten wzór będzie wyglądał mając takie dane Mam odcinek o współrzędnych A (1,1) i B (2,2) Mam punkt o współrzędnych P (1,0)

MQ: W liczniku masz iloczyn skalarny.

	1
U ciebie wychodzi −		, więc najbliższy punkt to A.
	2

PW: W tym konkretnym przypadku podanym o 14:19 należałoby: a) zauważyć, że końce odcinka AB (a więc i cały odcinek) leżą na prostej o równaniu y = x. Inaczej mówiąc: każdy punkt Q odcinka ma AB ma postać Q = (t,t), t∊[1,2]; b) policzyć |PQ| = √(t−1)²+(t−0)² = √2t²−2t+1, t∊[1,2]; c) znaleźć minimum funkcji f(t) = √2t²−2t+1, t∊[1,2]; minimum to jest najmniejszą z odległości |PQ|, czyli odległością P od AB.

Saizou : widzę że już daliście sobie radę xd

tomker: Dzięki MQ i Gotowiec. Dokładnie tak. Sprawdziłem to na różnych wariantach. PW też dziękuję.

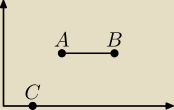
tomker: Mam problem z określeniem współczynnika podanego przez MQ Gdy odcinek jest bezpośrednio równoległy do osi X lub Y, to współczynnika nie da się obliczyć. Jak odcinek jest pod lekkim kątem, to współczynnik da się określić. NP. Współrzędne A(2,2) B(3,2) C(1,0) Jak mam temu zaradzić

PW: Analogicznie do sposobu z 16:13. Odcinek AB to zbiór punktów Q: Q = (t,2), t∊[2,3]. Liczyć |CQ|, znaleźć minimum.

tomker: Jestem laikiem, nie każcie mi znowu cały dzień szukać w internecie wyjaśnienia waszych wzorów. To co podał mi MQ musiałem przez następne parę godzin rozszyfrowywać. Nie jestem matematykiem i nie rozumiem wszystkich wzorów. Jestem dobry w innych dziedzinach, w których wy zapewne nie macie pojęcia, ale wytłumaczyłbym wam łopatologicznie zagadnienia na których wy się nie znacie. Czy mogę liczyć na bardziej przyjazną pomoc?

PW: W swoim rysunku z 22:48 dorysuj dowolny punkt Q na odcinku AB i zrzutuj go na oś OX − uzyskasz punkt Q'. Odległość |CQ| jest przeciwprostokątną trójkąta CQ'Q. Za każdym razem otrzymamy trójkąt prostokątny o tej samej długości przyprostokątnej Q'Q (bo odcinek AB jest równoległy do osi OX). Druga przyprostokątna CQ' jest zmienna − tym większa, im bliżej punktu B znajdzie się Q. Najkrótsza przyprostokątna CQ' będzie wtedy, gdy Q=A. Wniosek: najkrótszy odcinek łączący C z punktami odcinka AB to odcinek CA

tomker: Dzięki PW, jutro (w zasadzie już dzisiaj rano) to przeanalizuję

tomker: MQ: Wszystko jest OK z obliczeniami przy warunku z rysunku 22:48. Ja popełniłem błąd, przy obliczeniach. Tak to jest, jak się nie zajmuje matematyką na co dzień. Dziękuję wszystkim jeszcze raz.

MQ: @tomekr: Musisz być cierpliwy −− nie siedzimy kołkiem na forum i nie ślinimy się w oczekiwaniu na wpisy. Poza tym jest okres wakacyjny −− to też wydłuża czas reakcji. Co do problemu, to cieszę się, że sam doszedłeś do tego, gdzie twój błąd. I wierz mi −− nie czekałem specjalnie. Po prostu dopiero teraz tu zajrzałem.

MQ: A co do "łopatologicznego tłumaczenia", to unikniesz na przyszłość takich nieporozumień, gdy zawczasu określisz mniej więcej poziom, na jakim chcesz odpowiedzi (pomocy). Moim zdaniem akurat ten problem wyszedł ci w sumie na dobre −− dzięki własnej dociekliwości poszerzyłeś chyba trochę swoją wiedzę matematyczną o elementy rachunku wektorowego

tomker: @MQ: O tak. Wierz mi, wiem teraz więcej o wektorach niż w liceum