2 zadania z wart. bezwzgledna gad:

	1
bardzo bym prosil o wytlumaczenie 2 przykladow krok po kroku :		≥ −2
	|5x − 1|

|2x − 3|
	≤ 2
|x −2|

WueR: |5x−1|>0,

1
	≥ −2 ⇔ 1 ≥ −2|5x−1|
|5x−1|

Mila: 1)

1
	≥−2
|5x−1|

	1
5x−1≠0⇔x≠
	5

|5x−1|>0 z definicji wartości bezwzględej i założenia ⇔

1
	>0 dla każdego x∊D, to tym bardziej jest większe od ujemnej liczby −2.
|5x−1|

	1
odp. x∊R\{		}
	5

Mila: 2)

|2x−3|
	≤2
|x−2|

	3
|2x−3|≠0⇔x≠
	2

|2x−3|
	≤2 /*|x−2| ⇔
|x−2|

|2x−3|≤2*|x−2| obie strony nierówności są nieujemne, to podnosimy obustronnie do kwadratu (2x−3)²≤4*(x−2)² 4x²−12x+9≤4* (x²−4x+4) 4x²−12x+9≤4x²−16x+16⇔ −12x+16x≤16−9 4x≤7

	7		3
x≤		i x≠
	4		2

Zapisz jako sumę przedziałów, potrafisz?

Radek: Zajrzy tu Pani ? https://matematykaszkolna.pl/forum/255375.html

gad: jasne ze potrafie ok , jeszcze jeden przyklad podobny , zebym mial porownanie do poprzedniego :

|x − 1|
	> 1 , a przyklad numer 2 da sie zrobic innym sposbem ?
|x + 1|

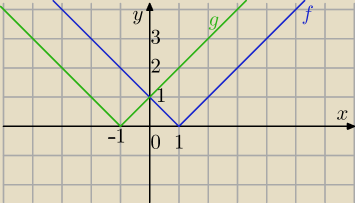
Mila: Można rozważać w przedziałach. To będzie więcej rachunków. Można graficznie. 3) |x+1|≠0⇔ x≠−1

|x−1|
	>1 /*|x+1|
|x+1|

|x−1|>|x+1| /² x²−2x+1>x²+2x+1 −4x>0 /:(−4) x<0 Metoda graficzna f(x)=|x−1| g(x)=|x+1| f(x)>g(x) Niebieski wykres leży nad zielonym wykresem dla x<0 Dobranoc

Mila: Myślałam, że tu spojrzysz i zauważysz, że (−1) nie należy do dziedziny nierówności. Należy pamiętać o dziedzinie nierówności.(równania) D=R\{−1} Odp. x∊(−∞,−1)∪(−1,0)