logarytmy tyu: ma ktoś pomysł jak to w ogóle zacząć liczyć wykaż, że równanie log₃(x−2) −2 log₉(x+1)=m+1 m∊R ma rozwiązanie

	1		1
należące do przedziału <3,5> dla parametru m∊ < log3		; log3		>
	12		6

Kacper: Zacznij od dziedziny i postaraj się wyznaczyć "x" z równania

tyu: ok

tyu: te zadania z parametrem mnie dobijają

tyu: to zadanie wymaga chyba zastosowanie wzoru, którego nie ma w tablicach

	m
logambn=		logab
	n

Saizou : tyu ale ten wzór wynika ze wzorów, które są w tablicach xd

Saizou : ale pokręciłeś/łaś ten wzór

	k
logambk=		logab
	m

tyu: a czy na maturze − w stresie i pośpiechu − jest czas na wyprowadzanie wzorów.

	n
po prawej stronie ma być ...=		logab
	m

Saizou : wyprowadzenie wzorku to 1 min

	logcbk		k*logcb		k
logambk=		=		=		logab
	logcam		m*logca		m

tyu: zapiszę to sobie, może łatwiej mi utrwali się w pamięci. Dziękuję za wyprowadzenie.

Saizou : ja w sumie tego nie wyprowadziłem, tylko przekształciłem za pomocą wzorów z karty xd

tyu: wyszło mi coś takiego

x−2
	= 3m+1
x+1

	x−2
g(x)=		to chyba f. homograficzna
	x+1

f(x)= 3^m+1 to jest chyba y= 3^m przesunięte o u[−1;0]

Saizou : pójdź dalej i wylicz 'x'

tyu: ale jak? przecież nie pomnożę stronami przez x+1

Saizou : dlaczego nie ?

tyu: miało być "przez (x+1)² "

tyu: racja bo x>2

razor: Równanie można mnożyć przez wszystko co nie jest zerem Tylko przy nierównościach musimy znać znak

Saizou : ale zresztą przecież to równanie a nie nierówność, równania możesz mnożyć przez mianowniki, bez zapewnienia sobie czy to jest dodatnie czy ujemne xd

tyu: x=3^m+1 + 2 , czyli 3^m przesunięte o u[−1;2]

razor: sprawdź rachunki

tyu: zaraz je przepiszę

tyu: 1/ log₃(x−2)− 2log₉(x+1)=m+1 i

	2
2/ 2log9(x+1)= log32(x+1)2=		log3(x+1) = log3(x+1)
	2

więc 3/ log₃(x−2)− log₃(x+1) =m+1

	(x−2)
4/ log3		= m+1
	(x+1)

	(x−2)
5/ log3		= log33m+1
	(x+1)

	x−2
6/		= 3m+1
	x+1

pigor: ..., no to jutro ... jak się wyśpisz wyznacz stąd x=f(m); wtedy jeszcze tylko nierówność 3≤ x ≤ 5, czyli 3≤ f(m) ≤5 i tyle .

Eta: No to jedziemy dalej D : x>2

	2+3m+1
7/ x−2=3m+1*x+3m+1 ⇒ x=		i x>2
	1−3m+1

zatem mianownik musi być dodatni , bo licznik jest dodatni teraz rozważamy x∊<3,5> otrzymujemy układ nierówności:

	2+3m+1		2+3m+1
3≤		⋀		≤5
	1−3m+1		1−3m+1

dla 1−3^m+1>0 możesz mnożyć przez 1−3^m+1 bez zmiany zwrotu nierówności spróbuj dokończyć ...... i otrzymasz poprawną odpowiedź

Eta: @pigor zobacz https://matematykaszkolna.pl/forum/255336.html

Mila:

	x+1−3
g(x)=
	x+1

	−3
g(x)=		+1
	x+1

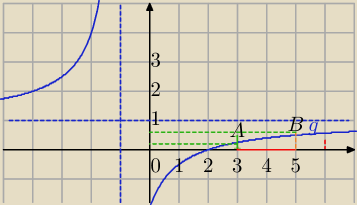
y=3^m+1 funkcja stała, ma przeciąć wykres g(x) na łuku AB, aby równanie :

x−2
	=3m+1 miało rozwiązanie należące do przedziału <3,5>
x+1

Obliczymy dla jakich wartości

	3−2		1
g(3)=		=
	3+1		4

	5−2		3		1
g(5)=		=		=
	5+1		6		2

1		1
	<3m+1<		⇔
4		2

1		1
	<3*3m<		/:3
4		2

1		1
	<3m<		logarytmujemy
12		6

	1		1
log3(		)<log3(3m)<log3(		)⇔
	12		6

	1		1
log3(		)<m<log3(		)
	12		6

cnw ==============================

Eta:

Mila: dla Ety

pigor: ..., widziałem i pozostawię ... bez komentarza , bo kto w szkole uczy (słyszał) obecnie o syntetycznym (od synteza) podejściu do rozwiązania szkolnych zadań geometrii elementarnej; jestem w każdym razie ... za .

Eta:

tyu: dziękuję wszystkim za pomoc i zainteresowanie Eta w Twoim rozwiązaniu (użyję "modnego" dzisiaj słowa) nie ogarniam przez co został przemnożony ułamek w siódmej linii po znaku "⇒" Mila w Twoim rozwiązaniu najpierw przekształcasz tą f. homograficzną do takiej postaci, by można ją była narysować, bo od razu można podstawiać za x liczbę 3 i 5, do postaci f. homograficznej z linii szóstej To rozwiązanie jest bardziej zrozumiałe dla mnie. Dzięki raz jeszcze. Jutro przepiszę do kajetu.

Mila: Na zdrowie Dobranoc.

Eta:

	x−2
7/		= 3m+1 /*(x+1)≠0 bo x>2
	x+1

x−2=(x+1)*3^m+1 x−2=3^m+1*x+3^m+1 x−3^m+1*x=2+3^m+1 x(1−3^m+1)=2+3^m+1

	2+3m+1
x=
	1−3m+1

Teraz już jasne?

tyu: tak, teraz rozumiem. Dziękuję.

mono: