wykaż Eta:

	1
Wykaż,że |∡ABD|=		|∡ABC|
	3

Pomocy

Saizou : Etuś co za spam robisz na forum

Eta: Hej Mila

Mila:

Eta: Jaki spam? ........ potrzebuję pomocy Pomożesz Saizou ? plisss

Saizou : Eta poszukaj w archiwum już kiedyś to rozwiązywałaś

Eta: Nie pamiętam

Eta:

Kacper: Z rysunku tego nie widać

Hugo: Mila, Eta

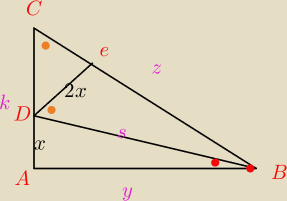
Hugo: z tw cosinusów x²=y²+s² −2cos|∡ABD|*y*s k²=e²+y²−2ey*cos|∡ABC| dzielimy

x2=y2+s2 −2cos|∡ABD|*y*s
k2=e2+y2−2ey*cos|∡ABC|

tr. DEB♥∫ z tw cos 4x²=s²+z²−2zscos DBC i tu mamy zależność że konty ABC= ABD+DBC musze uciekać na rowerki 60km robimy

5-latek: Hugus kąty a nie konty

pigor: ..., a mnie brakuje jednak oryginalnej treści zadania, aby ... bez straty czasu pochylić się nad tym ... ładnym, ale dla mnie niestety nie jednoznacznym rysunkiem . ...

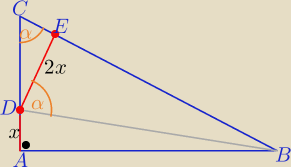
Eta: Hej π.. No właśnie.... Taka jest treść zadania: W trójkącie prostokątnym ABC, kąt przy wierzchołku A jest prosty i |∡ACB|=α Na bokach AC i BC obrano odpowiednio punkty D i E tak,że |DE|=2|AD| i |∡BDE|=α

	1
Wykaż,że |∡ABD|=		|∡ABC|
	3

matyk: mogę zapytać skąd to zadanie?

bezendu: KobiEta wymyśla takie zadania w wolnej chwili

matyk: Gdyby je wymyśliła to znałaby rozwiązanie

Metis: Jesteś w błędzie @matyk'u

pigor: ... W trójkącie prostokątnym ABC, kąt przy wierzchołku A jest prosty i |∡ACB|=α Na bokach AC i BC obrano odpowiednio punkty D i E tak, że |DE|=2|AD| i |∡BDE|=α. Wykaż, że |∡ABD|= ¹₃|∡ABC|. −−−−−−−−−−−−−−−−−−−− widzę to np. tak: niech na rys.Ety − dla uproszczenia zapisu − − |∡CBD|=β, |∡ABD|=γ, to |∡ABC|=β+γ=90^o−α, a stąd suma kątów (*) α+β=90−γ=|∡CED| − miara kąta zewnętrznego ΔBDE, no to kolejno: z ΔABD: (**) x= |BD|sinγ, a z tw. sinusów w ΔCDE i ΔBDC odpowiednio :

|CD|		2x		|CD|		|BD|
	=		i		=		/ : stronami ⇒
sin(α+β)		sinα		sinβ		sinα

	sinβ		2x		sinβ
⇒		=		, stąd i z (**)		= 2sinγ ⇔
	sin(α+β)		|BD|		sin(α+β)

⇔ sinβ= 2sinγ sin(α+β), stąd i z (*) : sinβ= 2sinγ sin(90−γ) ⇔ ⇔ sinβ=2sinγcosγ ⇔ sinβ= sin2γ ⇒ β= 2γ /+γ ⇒ β+γ= 3γ ⇔ ⇔ |∡ABC|=3|∡ABD| ⇔ |∡ABD| = ¹₃|∡ABC| c.n.w. . ...

matyk: poszedłem auto umyć i posprzątać a tu pigor wrzucił rozwiązanie to ja już nie muszę, bo ten sam pomysł w miarę miałem (tw. sinusów)

pigor: ..., znam to ...

Eta: dla π..

diana7: Rozwiązanie syntetyczne: Niech ∡DBA=β oraz niech M leży na przedłużeniu odcinka CA poza punkt A, przy czym AM=DA. Liczymy sobie kąty i mamy, że ∡CDE=∡MBE, zatem czworokąt DEBM jest cykliczny, stąd ponieważ DE=DM, więc z tw. o kątach wpisanych opartych na tym samym łuku mamy:∡DBE=∡DME=∡DEM=∡DBM, co kończy dowód.

Mila: Pomysł dobry, ale masz błędy w zapisie.

diana7: Jakie błędy w zapisie ?

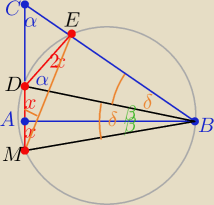
Eta: Ładny sposób rozwiązania .. diana7 To teraz jeszcze dołączę rysunek Czworokąt DEBM cykliczny ( taki, na którym można opisać okrąg) |DM|=DE|=2x, x>0 ΔMBD równoramienny zatem |∡ABM|=|∡ABD|=β Trójkąty DBM i DBE są przystające ⇒ |∡DBM|=|∡DBE|=δ oraz δ=2β

	1
to |∡ABC|=3β zatem |∡ABD|=		|∡ABC|
	3

c.n.w Pozdrawiam

Mila: W porządku diana, trochę inaczej oznaczyłam, bo sposób mam trochę inny, ale też z kątami. Przepraszam.

Mila: Nie wpisuję rozwiązania, bo byłby nadmiar, a niewiele różni się od waszego. Ja uzasadniam ,że suma kątów : |∡EDM|+|∡EBM|=180^o, ⇔na czworokącie MBED można opisać okrąg, dalej Kąty wpisane : ∡MBD=∡DBE są oparte na takim samym łuku. (cięciwy: |DM|=|DE|=2x) dalej już proste. dla diany

nie wiem: Dlaczego można opisać okrąg na tym czworokącie?

Mila: Sumy miar kątów przeciwległych czworokąta MBED mają po 180 ^o.

mono:

Hugo: Mila Eta !

mono: I Huguś

nie wiem: Ale dlaczego?:(

Mila: Nie wiem, czy nie znasz twierdzenia, czy nie wiesz dlaczego |∡EDM|+|∡EBM|=180^o ? Co mam wyjaśnić?

Eta: https://matematykaszkolna.pl/strona/872.html

nie wiem: Nie wiem dlaczego ta suma wynosi 180 twierdzenie znam

pigor: ... kąt wpisany oparty na średnicy (półokręgu) ma miarę 90^o, zatem

Hugo: Witajcie !

nie wiem: a gdzie jest ta średnica i kąt? może mi ktoś to wytłumaczyć?

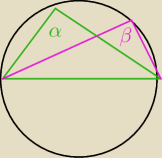
J: Każdy kąt oparty na średnicy okręgu ma miarę 90^o, bo jest to kąt wpisany oparty na tym samym łuku co kąt środkowy, a ten wynosi 180^o ( kąt wpisany jest zawsze połową kąta środkowego, gdy te kąty są oparte na tym samym łuku

Hugo: Eta to w przyszłym roku 100% z matury ?

nie wiem: nadal nie widzę związku z zadaniem. Gdzie tu mamy średnicę okręgu i kąty proste?

nienwiem: Nikt nie potrafi wytłumaczyć?

pigor: ..., średnicą to bok DB na rys. Ety (22:43), a kąty wpisane = 90^o oparte na niej ramionami o wierzchołkach E i M na okręgu to ∡BED i ∡BMD odpowiednio .

Mila: Już tłumaczę.Patrz rysunek 22:43, 20 lipiec. ∡BDM=α+δ jako kąt zewnętrzny ΔBCD. ΔBDM − Δrównoramienny, AB dzieli kąt przy wierzchołku B na połowy.(β− połowa kąta) W ΔBAD: ∡BDM+β=90^o⇔ α+δ+β=90^o Suma katów : |∡EDM|+|∡EBM|=(α+α+δ)+δ+β+β=2α+2δ+2β=2*(α+δ+β)=2*90^o=180. Ponieważ suma miar kątów w czworokącie jest równa 360, to suma miar pozostałych dwóch kątów też jest równa 180^o.

nie wiem : dzięki Mila pigor wg mnie twoje uzasadnienie jest błędne, bo odcinek BD wg mnie nie jest średnicą okręgu. Środek okręgu zawiera się w odcinku AD, czyli nie może być tak jak piszesz

Mila: W AD też nie .

nie wiem : dlaczego? skoro to symetralna odcinka? (jej fragment) a na tym trójkącie jest opisany okrąg

Mila: AB jest symetralną odcinka DM.

nie wiem : a na trójkącie DBM jest opisany okrąg, czyli na tej symetralnej znajduje się jego środek?

nie wiem : chodziło mi oczywiście o AB od początku

Mila: Właśnie to sprostowałam. Na tej symetralnej , czyli na AB jest środek okręgu opisanego.