lagarytmy tyu: Wyznacz wszystkie wartości parametru m, dla których równanie 2log(x + 3)=log(mx) ma tylko jedno rozwiązanie. Odpowiedź to m=12 lub m∊(−∞;0) Tutaj https://matematykaszkolna.pl/forum/24211.html Eta rozwiązała je, ale wyszło jej tylko m=12. Z kolei tutaj http://www.matematyka.pl/204290.htm jest rozwiązanie, którego nie rozumiem do końca. Rozumiem tylko, ze są rozpatrywane dwa przedziały (−3;0) (0;+∞). Ale dlaczego są one rozpatrywane w dwóch przedziałach.

pigor: ..., z własności funkcji y=logx i warunków zadania : x+3>0 i mx>0 i log(x+3)²= logmx ⇔ ⇔ x>−3 i [(m>0 i x>0) v (m<0 i x<0)] i (x+3)²= mx ⇔ ⇔ (m>0 i x>0 i x²+6x−mx+9=0) v (m<0 i −3<x<0 i x²+6x−mx+9=0) ⇔ ⇔ [m>0 i x>0 i x²+(6−m)x+9=0] v (m<0 i −3<x<0 i x²+(6−m)x+9=0} ⇔ ⇔ [m>0 i x>0 i x²+(6−m)x+9=0] v (m<0 i −3<x<0 i x²+(6−m)x+9=0} ⇒ ⇒ [m>0 i x>0 i Δ=(6−m)²−36=0 i c=9>0] v (m<0 i −3<x<0 i Δ>0) ⇔ ⇔ (m>0 i x>0 i m(m−12)=0 i c=9>0) v (m<0 i −3<x<0 i m(m−12)>0 i c=9) ⇔ ⇔ (m=12 >0 i x>0) v (m<0 i −3<x<0) ⇒ m∊{12} U {−∞;0) . ...

lolek: przecież 0 być nie może...

daras: lolek nie znasz się

tyu: dziękuje pigor za rozwiązanie. Zaraz wrócę do tego zadania.

tyu: mam pytanie dotyczące trzeciej linii od dołu "m>0 i x>0 i Δ=(6−m)²−36=0 . v m<0 i −3<x<0 i Δ>0" na początku jest warunek mx>0 zatem jest on rozpisany na dwa warunki 1/ m>0 i x>0 v 2/ m<0 i x<0 ale jest warunek x+3>0 wiec x>−3 zatem ostatecznie m<0 i −3<x<0 tylko dlaczego gdy 1/ m>0 i x>0 to Δ=0 gdy 2/ m<0 i −3<x<0 to Δ>0 chyba w obu przypadkach ma być Δ=0 jeśli ma być tylko jedno rozwiązanie

tyu: czy chodzi tutaj o to, że w przypadku Δ>0 są dwa rozwiązania, ale tylko jedno należy do dziedziny a gdy jest Δ=0 czyli jest jedno rozwiązanie, które należy do dziedziny. ktokolwiek coś podpowie

tyu: a może ktoś się skusi na wytłumaczenie

Kacper: Jutro ci rozwiąże moim sposobem

tyu: w piątek wszyscy chyba balują

daras: ja nie baluję tylko gram w karty i oglądam Ave maria

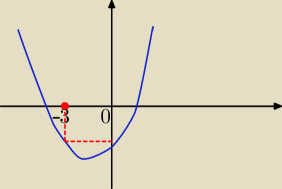
zan: Ja też nie baluję Dziedzina : x∊(−3,∞) i [(m>0 ⋀x>0) ⋁(m<0⋀x<0)] mamy dwa przypadki: 1^o x∊(0,∞) i m>0 , 2^o x∊(−3,0) i m<0 1^o log(x+3)²=log(mx) ⇒ x²+(6−m(x+9=0 jedno rozwiązanie dla Δ=0 ⇒ m(m−12)=0 ⇒ m=12 2^o x²+(6−m)x+9=0 ma jedno rozwiązanie z przedziału (−3,0) gdy : Δ>0 i f(−3)<0 lub Δ>0 i f(0)<0 , ale f(0) =9>0 to : Δ>0 ⇒ m∊(−∞,0)U (12,∞) f(−3) <0 ⇒ 9−18+3m+9<0 ⇒ m<0⇒m∊(−∞, 0) Odp: m∊(−∞,0) U{12}

tyu: dziękuję zan za rozwiązanie. Jednak czy mógłbym prosić o odpowiedź na moje pytania z postu z godziny 18.25 z 18 lipca 2014 r. Bo kolejny sposób na rozwiązania tego zadania mi nie pomoże, jeśli nie będę znał odpowiedzi na te pytania.