logarytmy tyu: proszę o wskazanie błędu 1/ log₃x+ log²₃x+ log³₃x+...<1 2/ q=a₁=log₃x S<1

	log3x
3/		<1 i t=log3x
	1− log3x

	t		t		1−t
4/		<1		− (		) <0
	1− t		1− t		1− t

5/ 0< 2t²−3t+1

	1		1
6/ t1=		t2=1 t∊(−∞;		) u (1;+∞)
	2		2

	1
7/ log3x<		log3x<log3√3 x<√3
	2

8/ log₃x>1 log₃x> log₃3 x>3

	1
a wynik to x∊(		;√3 ) czyli źle wyliczyłem pierwiastki, ale gdzie jest błąd
	3

Janek191: log₃ x = q więc I log₃ x I < 1

tyu: a dlaczego jest taka zależność I log₃ x I < 1 bo nie rozumiem

Janek191: Suma nieskończonego ciągu geometrycznego

	a1
S =		, gdy I q I < 1
	1 − q

tyu: Dziękuję za zainteresowanie. Mam pytanie − czy w każdym zadaniu z ciągów, których wyrazami są logarytmy, trzeba robić takie założenie Np tu https://matematykaszkolna.pl/forum/255239.html też

Janek191: Jeżeli mamy sumę nieskończonego ciągu geometrycznego o ilorazie q, to musi być I q I < 1 W podanym przykładzie − też Do logarytmów i funkcji trygonometrycznych musimy zastosować dodatkowe założenia.

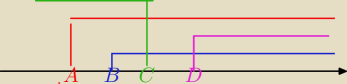
tyu: czyli dochodzi jeszcze log₃x<1 v log₃x>−1

	1
log3x<log33 v log3x> log3
	3

	1
x<3 v x>
	3

	1
A=
	3

B= 1 C= √3 D= 3

tyu: ale nadal nie wiem, czy dobrze robię

Janek191: Nie ∨ , tylko ∧

Janek191: a₁ = log₃ x ; x > 0 q = log₃ x , więc − 1 < log₃ x < 1

	log3 x
S =		< 1 ; t = log3 x − 1 < t < 1
	1 − log3 x

t
	< 1 / * ( 1 − t)2
1 − t

t*( 1 − t) < ( 1 − t)² t − t² < 1 − 2t + t² 0 < 1 − 3 t + 2t² 2 t² − 3 t + 1 > 0 itd.

Janek191: Wychodzi, że x ∊ ( ¹₃; √3 )

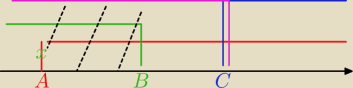
tyu: wyszedł mi prawidłowy wynik, ale proszę o sprawdzenie rysunku, czy taki powinien wyjść

	1
A=
	3

B= √3 C=3 (liczbę 3 mam z dwóch nierówności, więc mam ją w dwóch przypadkach x > 3 i x<3)

Janek191: Czy wszystko już jasne ?

Janek191: Skąd to 3 ?

tyu: tak, mam nadzieję, że tak. Dziękuję

tyu:

	1
no bo jest po rozwiązaniu nierówności t∊(−∞;		) u (1, +∞)
	2

czyli t< 0,5 i t>1 log₃x>1 log₃x>log₃3 x>3 to jeden przypadek

tyu: a drugi przypadek to q<1 i q>−1 zatem log₃x<1 log₃x<log₃3 x<3

tyu: czy ta trójka nie powinna tu wyjść

Janek191: 2 t² − 3 t + 1 > 0 Δ = 9 − 4*2*1` = 1

	3 − 1		1		3 + 1
t =		=		lub t =		= 1 − odpada, bo t ma być < 1
	4		2		4

Mamy zatem

	1
t <		i t > − 1 − z założenia
	2

czyli log₃ x < 0,5 ⇒ log₃ x < 0,5 log₃ 3 = log₃ √3 ⇒ x < √3 oraz

	1		1
log3 x > − 1 ⇒ log3 x > − 1log3 3 = log3		⇒ x >
	3		3

	1
Odp. x ∊ (		; √3 )
	3

====================

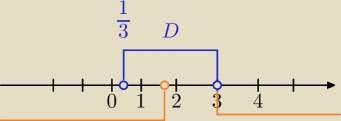
Mila: Abyś mógł obliczyć sumę nieskończonego ciągu geometrycznego, to musi być spełniony warunek |q|<1,

	a1
Wtedy S=		a jest to granica ciągu:
	1−q

	1−qn
Sn=a1*
	1−q

dla q, takiego, że |q|<1 mamy że lim_n→∞(qⁿ)=0 Ponieważ q w Twoim zadaniu wyraża się za pomocą logarytmu , to musisz dołączyć warunek na dziedzinę logarytmu. q=log₃(x) 1) x>0 i −1<log₃(x)<1⇔ log₃(x)>log₃(3⁻¹) i log₃(x)<log₃(3¹) i x>0⇔

	1
x>		i x<3 i x>0⇔
	3

D:

	1
x∊(		,3) i to jest dziedzina nierówności
	3

	log3(x)
2) S=		<1
	1−log3(x)

log₃(x)=t

t
	<1⇔
1−t

t
	−1<0⇔
1−t

t		1−t
	−		<0
1−t		1−t

t−1+t
	<0⇔
1−t

(2t−1)*(1−t)<0 parabola skierowana w dół⇔

	1
t<		lub t>1⇔
	2

	1
log3(x)<log3(31/2) lub log3(x)>log3(3) i x∊(		,3)⇔
	3

	1
(x<√3 lub x>3) i x∊(		,3)⇔
	3

	1
x∊(		,√3)
	3

tyu: teeeraz rozumiem. Czyli t ma być koniecznie mniejsze od 1. Dziękuję bardzo za pomoc

tyu: Czyli tutaj muszę dodać ten warunek na dziedzinę logarytmu i warunek IqI<1. Co da mi dziedzinę. A potem liczę sobie nierówność i rysuję parabolę i ma wynik. Dziękuję za pomoc Janek191 i Mila

Mila: Najpierw dziedzina, a potem rozwiązujemy równanie, czy nierówność.

tyu: a ja myślałem, że to takie proste Chociaż jak się wie o jak to liczyć to jest to proste

pigor: ..., cześć Mila ; pozdrawiam; no właśnie " Najpierw dziedzina, a potem rozwiązujemy równanie, czy nierówność." jestem całkowicie ZA i pozwól, że przy tej okazji dodam, że mówimy wtedy o metodzie równań (nierówności) równoważnych którą staram się jak najczęściej stosować ... ; jej przeciwieństwem jest metoda analizy starożytnych, którą stosuję w prostych przypadkach. ...

Mila: Witam pigor. Oczywiście masz rację pigor, czasem metoda starożytnych i sprawdzanie, najczęściej tam, gdzie kłopot z dziedziną . Ty to wyraźnie zawsze zaznaczasz i pięknie rozwiązujesz.

pigor: ..., dziękuję, ... staram się, a zawdzięczam, to starszemu bratu Jacek (Piotr) i mojemu nauczycielowi w L.O. prof. Zbigniew Chmielnicki .