może ktoś pomoże michał: rozwiąż równanie ^cosx_1−sinx + ^cosx_{1+ sinx} =0

sushi_ gg6397228: dziedzina, potem wspólny mianownik

Janek191: Napisz ułamki przy użyciu wielkiej litery U.

Random: Pozbądź się ułamków, mnożąc równanie obustronnie razy 1−sinx i 1 + sin x. Jako, że zero jest zz drugiej strony to zostanie ci cosx*(1−sinx+1−sinx)=0 2cosx=0 ⇒ cosx=0 ⇒ x=π/2 + kπ gdzie k ∊ C

Random: Pomyłka miało być w nawiasie (1+sinx+1−sinx). Ale i tak nie ma większego znaczenia. Teraz tylko pomyśl, które rozwiązania wyklucza dziedzina i koniec .

Mila: Z.

	π
sinx≠1 i sinx ≠−1⇔x≠		+kπ, k∊C
	2

cosx*(1+sinx)+cosx*(1−sinx)
	=0⇔
(1−sinx)*(1+sinx)

cosx+sinx cosx +cosx−sinx cosx
	=0⇔
(1−sinx)*(1+sinx)

2cosx=0 i x∊D

	π
x=		+kπ∉D ⇔brak rozwiązań.
	2

========================

michał: dziękuję ale mam jeszcze następujące zadania z ktorymi również mam kłopot w rozwiązywaniu 1 sin3x + cos3x = √2 2. cos2x + sin2x = 2x ∊ ≤ − 3π , ^π₂ ≥ proszę o rozwiązanie drugie nie ma rozwiązania

utem:

	√2
1) sin(3x)+cos(3x)=√2 /:
	2

√2		√2
	sin(3x)+		cos(3x)=1⇔
2		2

	π		π
sin(3x)*cos		+sin		cos(3x)=1⇔korzystamy z wzoru sin(α+β)=....
	4		4

	π
sin(3x+		)=1⇔
	4

	π		π
3x+		=		+2kπ⇔
	4		2

	π
3x=		+2kπ⇔
	4

	π		2kπ
x=		+
	12		3

=============

matura : Proszę o wypowiedzenie się tutaj.. https://matematykaszkolna.pl/forum/255179.html

Mila:

	√2
cos(2x) + sin(2x )= 2 /*
	2

√2		√2		√2
	cos(2x) +		sin(2x )=2*		⇔
2		2		2

	π		π
sin(		)*cos(2x)+sin(2x)*cos(		)=√2⇔
	4		4

	π
sin(2x+		)=√2 brak rozwiązania, bo √2>1, a wiemy że |sinα|≤1
	4

michał: w zadaniu 1−szym ma być przyrównane do 2 a nie do 1 i wtedy równanie ma postac sin(3x + ^π₄) = 2 i co dalej

Mila: Piszesz o przykładzie 20:37?

	√2
sin(3x)+cos(3x)=√2 /*
	2

	√2
tam obie strony mnożę przez		a zapisałam przez nieuwagę dzielenie.
	2

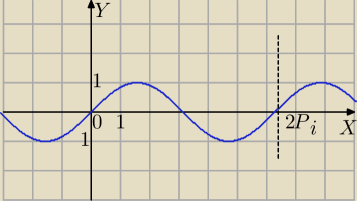
Mila: Gdyby tak było, jak napisałeś 21:24 to brak rozwiążań, bo |sinα|≤1 więc równanie

	π
sin(3x+		)=2 nie ma rozwiązań.
	4

Popatrz na wykres f(x)=sinx

michał: teraz się zgadza przepraszam bo mogłem się sam domyśleć za wykonanie zadań bardzo dziękuję jak napotkam na jakiś problem to znów się odezwę

Mila: