ciąg matura : oblicz granice

	2
lim n→∞(
	n+4

	2		2		2
lim=		=		=		ok ?
	4   n(1+ )   n		∞(1+0)		∞

jakubs:

	2   n*   n
limn→∞		=0
	4   n(1+ )   n

Mila: Po co tyle pisać?

	2
limn→∞		=0
	n+4

jakubs: W sumie tak

stała
	=0
∞

matura : ale dobrze to zrobiłam ?

Marcin:

2		2
	=		= 0 a nie można od razu?
∞+4		∞

Marcin: jooj. nie widziałem waszych wpisów, wybaczcie

matura : Mila skąd taki wniosek ? Ja dziś dopiero się tego uczę ?

zombi: To nie ucz się schematów, tylko pomyśl. W liczniku mamy stałą liczbę, natomiast mianownik cały czas rośnie, a im większy mianownik, tym mniejsza liczba, więc nasz ułamek stale maleje, do zera, którego jednak nigdy nie "dotknie".

Marcin: http://pl.wikipedia.org/wiki/Symbol_nieoznaczony Jeżeli masz jeden z symboli nieoznaczonych, to wtedy szukasz jakiejś metody.

matura : Mila skąd takie wnioski ?

jakubs: Przeczytaj co napisał zombi o 23:25.

matura : a czemu moje myślenie jest złe ?

jakubs: Według mnie jest Ok

Mila: matura, Twoje myślenie prawidłowe, ale przeczytaj co napisał zombi.

matura : czemu maleje do 0 cały ułamek ?

5-latek:

	2
np		=
	10

2
	=
100

2
	=
1000

2
	=
100000

2
	=
100000000

2
	=
100000000000

itd wiec do jakiej liczby dazy ten ulamek ?

Mila: Kreska ułamkowa oznacza dzielenie. Jeśli np. podzielisz 2 przez (10000000+4) , to otrzymasz małą liczbę, tym bardziej otrzymasz małą liczbę( dążącą do 0) jesli mianownik zwiększysz do nieskończoności , dodanie 4 nie ma już znaczenia.

5-latek: Dzien dobry Milu

matura : bo n∊N więc nie otrzymam liczny ujemnej tak ?

Soul Monster: Nie ponieważ N dąży do +∞.

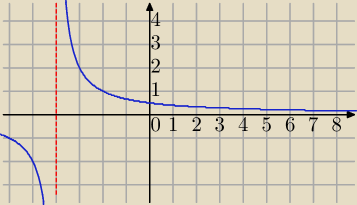
Mila: Zasada znaków w ilorazie jest Ci przecież znana. Wykres funkcji homograficznej też jest Ci znany.

	2
f(x)=
	x+4

Popatrz na wartości f(x) dla x∊N₊, dążą do zera.

Mila: Witaj 5−latek

matura : funkcja homograficzna. Już wszystko jasne, uczę się z kursu e−trapez. Dopiero zaczęłam jak dowiedziałem się, że mnie przyjęli Dziękuję.

Mila: Poczytaj: Analiza 1, Gewert, Skoczylas, jest w pdf.

matura : Robię zadania z tego kursu najpierw.

matura : Zobaczyłam tego skoczylasa.. Kresy, zbieżności co to jest wgl

jakubs: Ciągi mające granice nazywa się zbieżnymi, a pozostałe rozbieżnymi.

Mila: To jest teoria potrzebna do zrozumienia granic. Co będziesz studiować?

jakubs: http://pl.wikipedia.org/wiki/Granice_dolna_i_g%C3%B3rna

matura : Architekturę.

jakubs: Na YT poszukaj sobie Analiza matematyczna I wydane przez PWr. Dzięki nim już trochę się nauczyłem

5-latek: http://torrenty.org/torrent/579874 tam masz chyba 7 ksiazeczek i o ile pamietam to bedzie czesc 3 o granicach

matura : A po co podajesz mi jakieś książki ? Wystarczy internet i ten skoczylas od Mili. Chodzi mi tylko o zrozumienie granic

5-latek: Po to wlasnie zebys zrozumiala granice i jak sie takie granice liczy Tam masz pokazane krok po kroku jak sie liczy ale skoro nie chcesz to jak to mowia [P[Twoj cyrk twoje malpy]]

matura : Ja wiem jak sie robi krok po kroku ale pytałam o coś innego.

5-latek: jesli wiesz to poprosze Znajdz granice lim przy n−−−oo a_n= U{2n+1)(3n²+5}

	16n2+1
an= √		calosc po pierwiastkiem
	n2+7

5-latek:

	2n+1
Pierwszy ma byc an=
	3n2+5

matura :

	2n+1
limn→∞
	3n2+5

	1   n(2+ )   n
limn→∞=
	5   n2(3+ )   n2

	2
limn→∞=		=0
	n*3

5-latek: ja sie uczylem tak(dawno )

	oo
Dostaniemy synbol nieoznaczony
	oo

	wielomian
Mamy tak		wiec jesli dostajemy wyrazenie nieoznaczone wiec musimy
	wielomian

podzielic licznik i mianownik przez najwyzsza potego wystepujaca w mianowniku najwyzsza potega to n² wiec mamy pisze bez −−− oo

	2n/n2+1/n2
ale Ty w zeszycie pisz lim		= lim{2/n+1/n2}{3+5/n2}=
	3n2/n2+5?n2

	0
		=0
	3

matura :

	1
Co Ty za głupoty gadasz licznik 2n+1=n(2+		) n skróci się z n2 z mianownika i w liczniku
	2

zosatej 2 a nie 0

5-latek: A TY zrobilas tak patrz druga linijka licznik przeciez dostaniesz (oo) bo n−−−−oo wiec oo*2=oo a nie 2 to samo z mianownikiem przecie oo²= oo *3=oo bo 1/n i 5/n² dazy do zera i to nie bedzie Twoja 3 linijka tak jak napisalas

matura :

n		1
	=		więc nie dostanę w liczniku ∞ działania na potęgach...
n2		n

5-latek: Wiec tak patrz teraz na swoj post z 19:19 druga linijka

	1		1
na licznik przy n −−−oo masz tak n(2+		to oo(2+0) bo		dazy do 0 Tak ?
	n		n

wobec tego masz oo*2= oo Tak ?

	5		5
mianownik n2(3+		) n2 dazy do oo 3 wiadomo		dazy do 0 bo stala przez
	n2		n2

niewskonczonosc dazy do 0 wiec masz oo*(3+0)=oo*3= dalej nieskonczonosc

	oo
Wiec w drugiej linijce pokazales tyle ze to =		i tego nawet nie bylo ptrzeby tak
	oo

rozpisywac .bo juzw pierwszyj liniujce to widac (jak rozwiazesz kilkanascie przykladow jeszce to bedziesz widziec od razu )

	oo
Wiec trzecia linujka Twoja powinna byc lim−−−oo =
	oo

Teraz dopiero dzielisz licznik i mianownik przez najwyzsza potege mianownika

matura : Nie prawda. ! https://matematykaszkolna.pl/strona/312.html tutaj podobny przykład https://matematykaszkolna.pl/forum/forum.py?komentarzdo=312 Dobrze zrobiłam, więc nie wmawiaj, że mam źle i coś mam poprawiać Przykładu z pierwiastkiem nie wiem

Soul Monster: Matura "Co ty za głupoty gadasz" Naucz się, opanuj liczenie później obrażaj.

5-latek: Z pierwiastkiem to najpierw policz granice pod pierwiastkiem a potem wyciagnij z tego pierwiastek (wyjdzie ladna liczba −−− 4 )

matura : Nie obrażam nikgoo to raz, dwa dobrze zrobiłem, trzy nie wcinaj się skoro nie masz nic sensownego do powiedzenia...

matura :

	16n2+1
an=√
	n2+7

	1   n2(16+ )   n2
limn→∞√
	7   n2(1+ )   n2

lim_n→∞√16=4

5-latek: Teraz obrazilas . Wiec zyj sobie w swoim przekonaniu ze masz dobrze.

matura : Nawet wolfram pokazuje mi, że mam dobrze ale dobrze wmawiaj mi, że źle...

5-latek: Powiem to ostatni raz . Granica jest policzona dobrze bo ma wyjsc 4 i tego nie potrzeba wolframa (bo taka granice liczy sie w pamieci)

	oo
Zastanow sie jeszcze raz co dostaniesz w drugiej linijce czy dostaniesz √		czy
	oo

√16 . Na tym koniec podpowiedzi

MQ: Nie róbcie dziewczynie wody z mózgu −− dobrze liczy.

matura : Dziękuję w końcu ktoś potwierdził zamiast cały czas negować. dostanę √16=4

5-latek: MQ a le w trzeciej linijce nie dostanie z tego przeksztalcenia √16

matura : Jak to nie odstanę ?

1   n2(16+ )   n2
7   n2(1+ )   n2

	16+0
n2 się skróci ! i zostanie		=√16=4 ?
	1+0

5-latek: Dobrze . Ale dlaczego wyciagasz n² przed nawias

matura : żeby to skrócić... Metoda wyciągania największej potęgi przed nawias.

sushi_ gg6397228: przepis mówi, jeżeli wielomiany są tego samego stopnia, to po prostu spisuje się liczby stojące przy najwyższej potędze−−> to jest granica; po co zabawa z wyciąganiem przed nawias

5-latek: Ale przeciez ta metode mozesz stosowac gdy masz symbol nieoznaczony . A Ty nie pokazalas ze masz taki symbol . Wiec gdzie go masz ?

matura : Ale mogę wyciągnąc przed nawias.. 5−latek co Ty wgl mówisz.. Mogę wyciągnąć przed nawias...

matura : Niech ktoś w temacie odpowie na moje pytanie bo tutaj kilka wersji jest

matura : ?

5-latek: Mowie o tym np bez tego pierwiastka

	16n2+1		oo
lim−−−oo		=		bo 16n2 dazy do nieskonczonosci 1 do 1 i n2 dazy
	n2+7		oo

do nieskonczonosci i 7 do 7 . masz sybol nieoznaczony wiec teraz mozesz przeksztalcac dalej . Pytanie . czy w takiej granicy lim−−−oo 5n²+1 tez bedziesz wyciagala n² przed nawias ?Przeciez mozesz?

Mila: Mogą być takie rachunki. Zapisy doszlifujesz.

5-latek: Tak samo bedzie przy innych symbolach nieoznaczonych . Najpierw trzeba sprawdzic czy taki symbol wyjdzie i potem przeksztalcac

5-latek:

	∞
tam z 20:56 powinno byc zapisane prawidlowo =[		]
	∞

matura : Dziękuję. A 5−latek nadal swoje. Ja będę uczyć sie po swojemu skoro Mila i MQ mówią, że dobrze licze . Pozdrawiam

Mila:

	n2*(16+1/n2)
limn→∞√		=
	n2*(1+7/n2)

	16+1/n2
=limn→∞√		=
	1+7/n2

=√16=4 drugą linijkę można pominąć ( obliczyć w pamięci), od razu napisać trzecią.

matura : lim_n→∞5n²+1

	1
limn→∞n2(5+
	n2

lim_n→∞=∞ A kto mi zabroni wyciągać skoro dopiero się uczę ?

MQ: Ludzie, przecież dobrze liczy. Argumentowanie typu "Reguła mówi" tylko zabija inwencję! Ważne, żeby przekształcenia były poprawne matematycznie. @5−latek co do trzeciej linijki: nigdy nie robiłeś części rachunków (prostych czy oczywistych) w głowie? Przecież (niejawnie) skróciła sobie licznik i mianownik przez n². @matura 5−latkowi chodzi o to, że nie piszesz jawnie tego skracania przez n² i na maturze jakiś pop*** cyzelant może się do tego przyczepić. Wystarczyło 5−latek, żebyś jej tak to wytłumaczył i nie byłoby całej tej dyskusji.

Mila: matura, nikt tu nie chce Ci dokuczyć, nie trzeba tak emocjonalnie podchodzić. Spokojnie.

matura :

matura : Po prostu chcę się dobrze przygotować na studia i chcę mieć pewność, że dobrze robię, wolfram pokazuje dobrze, a 5−latek mówi że źle więc nie wiem i pytam się

Mila: Spokojnie, nie zrozumieliście się. Pisz swoje wątpliwości. Trochę ten edytor utrudnia niektóre zapisy.

matura : lim_n→∞4ⁿ−7ⁿ+3 ?

5-latek: MQ o to mi chodzilo . Skoro sie dopiero uczy to wedlug mnie powinna pisac kazde przeksztalcenie . Takie jest moje zdanie . Ja sie wlasnie tak uczylem . Ale moze kolezanka jest zdolniejsza niz ja

MQ: @5−latek OK, ja cię rozumiem, ale sam przyznasz, że nie wytłumaczyłeś jej zbyt zrozumiale, o co ci chodzi.

matura : ?

ICSP: wyciągnij 7ⁿ przed nawias.

matura : =−∞ ?

ICSP:

5-latek: W sumie to o nic . Zycze jej /jemu (post 19:56) powodzenia w nauce . Tyle

matura : Dzięki ICSP a pytanie kiedy korzystamy z tw o 3 ciągach ?

Mila: http://www.matemaks.pl/granica-ciagu.php?tid=10102

matura : Kolejny przykład

	−1
limn→∞(		−1)
	n+√n

	−1−n−√n
limn→∞
	n+√n

Teraz mnożyć przez sprzężenie ?

ICSP:

	−1
lim		=
	n + √n

Mila: Nie trzeba przekształcać.

	−1
limn→∞ (		)=0
	n+√n

	−1
limn→∞ (		−1)=0−1=−1
	n+√n

matura : Nie wpadłam na to, a można było zrobić tak jak pisałam ?

Mila: Niepotrzebna komplikacja.

matura : Jeszcze mam dwie trudne

	n!+(n+1)!
limn→∞		?
	n!+(n+2)!

MQ: Podziel licznik i mianownik przez n!

matura :

(n+1)!   1+   n!
(n+2)!   1+   n!

n!+(n+1)!
	i co ?
n!+(n+2)!

MQ:

	(n+1)!		(n+2)!
No ile jest		i
	n!		n!

matura : Już policzyłam, dziękuję

matura : wyszło 0