wyznacz wartość najwięk. funkcji... noga z matmy: wyznacz wartość największą i najmniejszą funkcji f(x) + x² − 4x + 3 dla x∊<−1;4>

ICSP: https://matematykaszkolna.pl/strona/1683.html

noga z matmy: x= −1 y= (−1)² − 4 * (−1) + 3= 1 +4+3=8 A(−1, 8) x= 4 y= 4² − 4*4+3= 16 − 19= −3 B(4,−3) Nie wiem jak dalej obliczyć wierzchołek , tego nie ogarniam mała pomoc proszę

ICSP: f(x) = ax² + bx + c

	−b
xw =		= ...
	2a

y_w = f(x_w) = ...

J:

	b		(−4)
xw = −		= −		= 2
	2a		2

ICSP: punkt B jest źle policzony.

J: Teraz policz: f(−1) =.... f(4) = .... f(2) = ...

noga z matmy:

	−b		−4		−4
xw=		=		=		to tak ma być ?
	2a		2*1		2

noga z matmy: o mama mia nie dam rady nie lubie tych funkcji

ICSP: b = −4

	−(−4)
xw =		= 2
	2

y_w = f(x_w) = ...

noga z matmy: bład w B ....B( 4,3) teraz zgadza się?

J: Patrz post 14:54 .... policz i wybierz najmniejszą i największą wartość.

ICSP: teraz jest

noga z matmy: cieszę sie chociaż błędu się dopatrzałam super już coś zaczynam lepiej rozumieć dziękuję za pomoc ..idę walczyć z tymi cyferkami

noga z matmy: czy ja mam to robić w ten sposób f(−1)= (−1)² − 4* (−1) +3 = ....tak?

ICSP: a odpowiedź ?

noga z matmy: odpowiedź wynosi f(−1)= 5

ICSP: f(1) było policzone dobrze. f(−1) = (−1)² − 4*(−1) + 3 = 1 + 4 + 3 = 8 f(4) = 3 f(2) = ... wartość minimalna = wartość maksymalna =

J: Nie.. f(−1) = 1 + 4 + 3 = 8 bo .. − 4*(−1) = 4

noga z matmy: f(2) = −15

J: Znowu źle...

noga z matmy: kurcze to ile? 5?

ICSP: pudło.

J: Pokaż obliczenia, to zobaczymy, gdzie robisz błąd.

noga z matmy: rany ale błąd zrobiłam już widze

noga z matmy: wynik to −1

ICSP: wreszcie Odp :

noga z matmy: haha głupi błą zamian 4*2 to podnosiłam 4²

noga z matmy: haha głupi błąd zamiast 4*2 to podnosiłam 4²

J: Teraz daj odpowieź do zadania.

noga z matmy: wartosc minimalna to −1 wartosc maksymalna to 8

ICSP:

noga z matmy: dziękuję za pomoc czy mogę prosić o pomoc w jeszcze 1 zadaniu ?

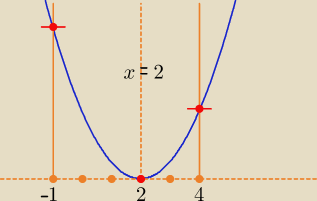
Bogdan: f(x) = x² − 4x + 3 Można naszkicować parabolkę bez układu współrzędnych, zaznaczyć oś symetrii x = x_w = 2, potem zaznaczyć proste x = −1 i x = 4. Od razu widać, że najmniejsza wartość jest dla x = 2, a największa dla x = −1, nie trzeba obliczać f(4): f(2) = 4 − 8 + 3 = −1, f(−1) = 1 + 4 + 3 = 8

J: Na oko ... to umarł gość w szpitalu...

ICSP: Bogdan jest tylko jeden problem : Jak uczeń w liceum ma naszkicować parabole mają daną postać ogólną funkcji kwadratowej ?

Bogdan: Jakie oko? Jeśli a > 0 to szkicujemy parabolę ramionami do góry bez układu współrzędnych i zaznaczamy

	b
oś symetrii x = xw = −		.
	2a

W arkuszach maturalnych takie zadanie występuje najczęściej jako zadanie zamknięte za 1 punkt, szkoda czasu na rozwlekłe obliczenia, prosty szkic załatwia sprawę. To nie jest szacowanie wyniku, a dokładne odwzorowanie sytuacji opisanej w zadaniu, od osi symetrii x = 2 do x = −1 są trzy jednostki, a do x = 2 są dwie jednostki, większa wartość jest więc dla x = −1, ponadto odcięta wierzchołka x = 2 należy do przedziału <−1, 4>, więc najmniejsza wartość jest dla x = 2. Chyba to jest oczywiste i co tu dużo liczyć.

noga z matmy: funkcja f(x)= −x² + bx + 4 przyjmuje największą wartość dla x=5. Oblicz f(−3)

Bogdan:

	b
−		= 5 ⇒ b = ...
	−2