Rachunek różniczkowy Blue: Mam dwa zadanka, których nie potrafię zrobić(oznaczone kółkami − 3 i 5): http://pl.tinypic.com/view.php?pic=m9pn54&s=8#.U6he1prwGM8 Liczę na Waszą życzliwość i pomoc

sushi_ gg6397228: zapisz przyklady a nie linkujesz

Blue: Czy w tym 3 zadaniu nie będzie tak, że granica lewostronna wynosi 1 , a prawostronna 2 i dlatego nie ma granicy w punkcie x=0?

Blue: sushi po co mam zapisywać przykłady skoro piąte zadanie wymaga zobaczenia rysunku? No może nie wymaga, ale na pewno jest to pomocne

sushi_ gg6397228: jestem bardzo leniwy i mi się nie chce klikać w odnośniki

Blue: Czyli jak przepisze treść, to powiesz mi czy dobrze myślę?Obiecujesz?

Blue:

	1		1		1
Wykaż, że funkcja f(x) = 2 dla x∊{1,		,		,		...} i f(x) = 1 dla x∊R\{1,
	2		3		4

	1
		,{1}{3},{1}{4}...}
	2

nie ma granicy w punkcie x=0 . Proszę bardzo!

Blue:

	1		1		1
nie napisałam "U" sorry: i f(x) = 1 dla x∊R\{1,		,		,		...}
	2		3		4

sushi_ gg6397228: nie dostałem odpowiedzi na stare zadania, w tym policzenie pochodnej złożonej, wiec nie wiem czy będę miał motywację

sushi_ gg6397228: definicja granicy ...

ICSP: sushi gg6397228 mój nowy mistrz

Blue: jakie zadania?

Blue: no granica jest w punkcie wtedy , jak jest lewostronna i prawostronna taka sama, czyż nie

sushi_ gg6397228: https://matematykaszkolna.pl/forum/254164.html w otoczeniu punktu "0" nawet jak przyjmiesz δ=0,00000000000000000000000000001 to otrzymasz wartości "1" i "2", a powinnaś otrzymać tylko jedną wartość

Blue: No ale odpowiedz na tamto zadanie jako tako otrzymałam, bo napisał je ICSP. A tego o czym potem pisałeś, to do dziś nie rozumiem, bo nie wiem , co to jest to In. Ale mniejsza z tym. Jeśli chodzi o to zadanie, to jak to napisać, aby to wykazać ? Wystarczy tak jak Ty powyżej?

Blue: czyli w końcu dobrze rozumuję to zadanie , czy nie? Że granica lewostronna i prawostronna są inne?

sushi_ gg6397228: zawsze można zrobić rysunek lub pokazać, ze istnieją dwa podciągi, co mają różne granice

Blue: Jezu sushi powiedz mi po prostu czy mam racje czy moje rozwiązanie jest złe . Tak lub nie (niepotrzebne skreślić)

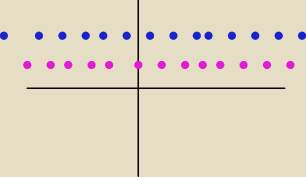
sushi_ gg6397228: masz w powiększeniu w nawiasie skala (10000000000000000000000000000000000000000000000000000000000000000000000000 0000000000000000000000000000000000000000000000000000000000000000000000000000 0000000000000000000000000000000000000000000000000000000000000000000000000000 0000000000000000000000000000000000000000000000000000 :1) i mi pokaż, te Twoje cudowne granice jednostronne ?

Blue: a to nie jest tak, że z lewej strony, czyli argumenty mniejsze od zera wszystkie mają wartość 1?

Blue: hmmm

Blue: i nastała cisza....

sushi_ gg6397228: no to masz lewą stronę (różowe− tylko) a prawa strona to masz dwukolor więc dalej masz "dwa podciągi" o dwóch różnych granicach

Blue: A ja nadal utrzymuje, że w takim przypadku można by wykorzystać granicę lewostronną i prawostronną

xx: No to pokaż jak?

Blue: limf(x) = 2 x−>0⁺ lim(fx) = 1 x−>0⁻

xx:

	1
a jak wezmę ciąg xn=		to zauważ, że
	nπ

f(x_n) =1 i x_n > 0 dla każdego x_n, więc lim_x→0⁺ f(x) = 1

Blue: Czyli jaką mam napisać odpowiedź, żeby to udowodnić? Możesz rozpisać wszystko?

Blue: ?

Blue: Mógłby ktoś pokazać te dwa ciągi, które mają inne granice?

Blue: Nikt nie pomoże?

zawodus: ciąg pierwszy

	1
(xn)=
	n

lim_{n →∞}(x_n) = x₀=0 lim_{n →∞}(f(x_n))=lim_n→∞2=2 teraz drugi wymyślasz i koniec

Blue:

	−1
a ten drugi to może być np.
	n

Blue: tak?

zawodus: tak

Blue: Wreszcie odpowiedziałeś Dzięki