 f(x) = a x2 + b x + c
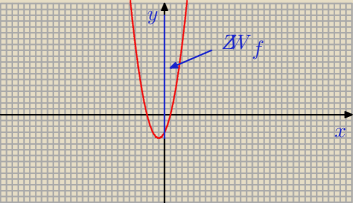
Jeżeli a > 0 , to ramiona paraboli ( wykresu tej funkcji ) skierowane są ku górze).
Wtedy zbiór wartości funkcji f jest równy
ZWf = < q ; + ∞ ) , gdzie W = ( p ; q ) − wierzchołek paraboli
Dla a < 0 jest odwrotnie : ZWf = ( − ∞ ; q >
Mamy
f(x) = x2 + 2 x − 3
czyli a = 1 > 0 b = 2 c = − 3
Należy obliczyć q
f(x) = a x2 + b x + c
Jeżeli a > 0 , to ramiona paraboli ( wykresu tej funkcji ) skierowane są ku górze).
Wtedy zbiór wartości funkcji f jest równy
ZWf = < q ; + ∞ ) , gdzie W = ( p ; q ) − wierzchołek paraboli
Dla a < 0 jest odwrotnie : ZWf = ( − ∞ ; q >
Mamy
f(x) = x2 + 2 x − 3
czyli a = 1 > 0 b = 2 c = − 3
Należy obliczyć q
| − Δ | ||
q = | ||
| 4 a |
| − 16 | ||
q = | = − 4 | |
| 4*1 |
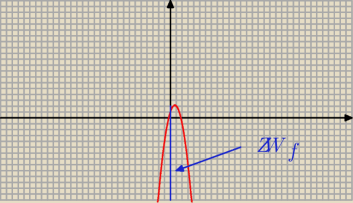 f(x) = − 2 x2 + 3x + 1
Δ = 32 − 4*(−2)*1 = 9 + 8 = 17
f(x) = − 2 x2 + 3x + 1
Δ = 32 − 4*(−2)*1 = 9 + 8 = 17
| − 17 | 17 | |||
q = | = | |||
| 4*(−2) | 8 |
| 17 | ||
ZWf = ( − ∞ ; | > | |
| 8 |

 tak :
y=x2+2x−3 ⇔ x2+2x−3−y=0 ⇒ Δ≥0 ⇔ 22−4(−3−y) ≥0 /:4 ⇔ 1+3+y ≥0 ⇔
⇔ y ≥ −4 , czyli Ef = [−4;+∞) − szukany zbiór wartości funkcji f.
−−−−−−−−−−−−−−−−−−−−−−−
lub np. ...
tak :
y=x2+2x−3 ⇔ x2+2x−3−y=0 ⇒ Δ≥0 ⇔ 22−4(−3−y) ≥0 /:4 ⇔ 1+3+y ≥0 ⇔
⇔ y ≥ −4 , czyli Ef = [−4;+∞) − szukany zbiór wartości funkcji f.
−−−−−−−−−−−−−−−−−−−−−−−
lub np. ... tak:
f(x)= x2+2x−3= x2+2x+1−4= (x+1)2−4 i a=1>0 ramiona paraboli w górę,
więc dla każdego x∊R f(x) ≥ −4 , czyli Ef = [−4;+∞) . ...
tak:
f(x)= x2+2x−3= x2+2x+1−4= (x+1)2−4 i a=1>0 ramiona paraboli w górę,
więc dla każdego x∊R f(x) ≥ −4 , czyli Ef = [−4;+∞) . ...