rownanie
pomocy: Jak rozwiazac rownanie cos2x=0 w przedziale [0, π] za pomoca kola trygonometrycznego?
16 cze 16:40
wredulus:
A w kole trygonometrycznym jak odczytuje sie wartosc cosinusa
<−−− pytanie−wskazowka
16 cze 16:43
pomocy: os OX odpowiada wartosci cosx
16 cze 17:02
pomocy: i co dalej?
16 cze 17:20
pomocy: nie ma roznicy czy jest cos2x czy cosx w przypadku kola trygonometrycznego?
16 cze 17:49
pomocy: ?
16 cze 17:59
pomocy: czyli jak to rozwiazac?
16 cze 18:33
Mila:
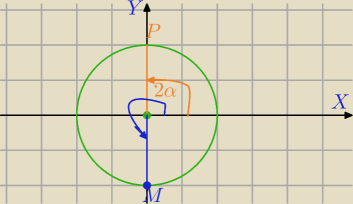
P=(0,r), M
| | x | | 0 | | π | | 3π | |
cos(2α)= |
| = |
| =0 dla 2α= |
| lub 2α= |
| |
| | r | | r | | 2 | | 2 | |
| | π | | 3 | |
cos(2α)=0⇔2α= |
| +2kπ lub 2α= |
| π+2kπ⇔ |
| | 2 | | 2 | |
16 cze 18:44
pomocy: dziekuje
16 cze 19:57
Mila:
16 cze 20:55
zadanie: | | π | |
a skad wiadomo, ze 2α= |
| ? |
| | 2 | |
17 cze 11:23
17 cze 11:30
zadanie: | | π | |
a skad wiadomo, ze cos |
| =0? |
| | 2 | |
17 cze 11:35
17 cze 11:37
zadanie: no dobrze ale mi chodzi na podstawie kola jednostkowego ?
17 cze 11:55
J:
Pytasz poważnie, czy się zgrywasz ...?
17 cze 12:04
zadanie: naprawde gdzie to widac na kole jednostkowym?
17 cze 12:07
J:
Dla kata 90
o ruchome ramię kąta pokrywa się z osią OY , zatem współrzędna x punkty P na
| | x | | 0 | |
ruchomym ramieniu kąta wynosi 0 , czyli cos90o = |
| = |
| = 0 |
| | r | | r | |
17 cze 12:13
zadanie: dziekuje
17 cze 12:19
zadanie: a jakby wygladala nierownosc cos2x>0 i cos2x<0 ? tez przy pomocy kola jednostkowego ?
17 cze 12:21
17 cze 12:26
zadanie: | | x | |
r jest zawsze wieksze od zera bo to promien wiec |
| >0 jezeli x>0 |
| | r | |
17 cze 12:51
J: Czyli ruchome ramię musi być w I −szej i IV −tej ćwiartce.
17 cze 12:56
zadanie: | | π | | 3 | |
cos2x>0 gdy x∊( |
| +2kπ, |
| π+2kπ) ? |
| | 2 | | 2 | |
17 cze 13:06
J:
cos2x > 0 ⇔ 2x ∊ ( − π/2 + 2kπ , π/2 + 2kπ ) ⇔ x ∊ ( − π/4 + kπ , π/4 + kπ)
17 cze 13:13
zadanie: dziekuje
17 cze 13:24
zadanie: cosx=0
| | π | |
ogolnie x= |
| +kπ ; k−calkowite |
| | 2 | |
cos2x=0
| | π | |
cosx>0 gdy x∊(0, |
| ) w przedziale [0, π] |
| | 2 | |
| | π | |
cos2x>0 gdy x∊(0, |
| ) w przedziale [0, π] |
| | 4 | |
| | π | |
cosx<0 gdy x∊( |
| , π) w przedziale [0, π] |
| | 2 | |
| | π | | π | |
cos2x<0 gdy x∊( |
| , |
| ) w przedziale [0, π] |
| | 4 | | 2 | |
dobrze?
17 cze 18:02
zadanie: ?
17 cze 18:31
zadanie: ?
17 cze 19:50